
What is the value of x? Enter your answer in the box.
x=

Answer
500.1k+ views
Hint: In order to find the value of $x$, assume the line ED to be the angle bisector of the angle E, Apply the angle bisector theorem to the triangle which states that the ratio of the sides is equal to the ratio of the side opposite to the angle bisected by the line ED.
Complete step-by-step answer:
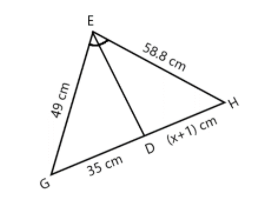
We are given with a figure of a triangle with the length of the sides such as:
$EG = 49{\text{ cm}}$
$EH = 58.8{\text{ cm}}$
$GD = 35{\text{ cm}}$
$DH = x + 1{\text{ cm}}$
Considering/ Assuming the line ED to be the angle bisector of the angle E. So, now, considering this we can apply the Angle bisector theorem. According to which the ratio of the sides of the line divided by the angle bisector ED is equal to the ratio of the remaining sides of the triangle.
According to this, the equation becomes:
$\dfrac{{EG}}{{EH}} = \dfrac{{GD}}{{DH}}$
Substituting the values of EG, EH, GD and DH according to the figure in the above value, and we get:
$ \Rightarrow \dfrac{{49}}{{58.8}} = \dfrac{{35}}{{x + 1}}$
Doing cross-multiplication:
$ \Rightarrow 49\left( {x + 1} \right) = 35 \times 58.8$
Opening the bracket on the left side and multiplying the values, we get:
$ \Rightarrow 49x + 49 = 2058$
Subtracting both sides by $49$ in the above equation:
$ \Rightarrow 49x + 49 - 49 = 2058 - 49$
$ \Rightarrow 49x = 2009$
Dividing both sides by $49$ in the above equation, and we get:
$ \Rightarrow \dfrac{{49x}}{{49}} = \dfrac{{2009}}{{49}}$
$ \Rightarrow x = 41$
Therefore, the value of $x$ obtained is $41$.
Note: Since, we were not given a situation on the triangle, so we assumed the line ED to be the angle bisector by ourselves to solve for x. If any other situation is given then take that, and do not assume anything.
Cross check your answer by substituting the value, in the above equation on angle bisector. If the ratio on both sides is the same, the value obtained is absolutely correct.
Complete step-by-step answer:
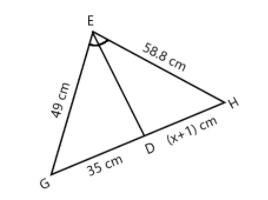
We are given with a figure of a triangle with the length of the sides such as:
$EG = 49{\text{ cm}}$
$EH = 58.8{\text{ cm}}$
$GD = 35{\text{ cm}}$
$DH = x + 1{\text{ cm}}$
Considering/ Assuming the line ED to be the angle bisector of the angle E. So, now, considering this we can apply the Angle bisector theorem. According to which the ratio of the sides of the line divided by the angle bisector ED is equal to the ratio of the remaining sides of the triangle.

According to this, the equation becomes:
$\dfrac{{EG}}{{EH}} = \dfrac{{GD}}{{DH}}$
Substituting the values of EG, EH, GD and DH according to the figure in the above value, and we get:
$ \Rightarrow \dfrac{{49}}{{58.8}} = \dfrac{{35}}{{x + 1}}$
Doing cross-multiplication:
$ \Rightarrow 49\left( {x + 1} \right) = 35 \times 58.8$
Opening the bracket on the left side and multiplying the values, we get:
$ \Rightarrow 49x + 49 = 2058$
Subtracting both sides by $49$ in the above equation:
$ \Rightarrow 49x + 49 - 49 = 2058 - 49$
$ \Rightarrow 49x = 2009$
Dividing both sides by $49$ in the above equation, and we get:
$ \Rightarrow \dfrac{{49x}}{{49}} = \dfrac{{2009}}{{49}}$
$ \Rightarrow x = 41$
Therefore, the value of $x$ obtained is $41$.
Note: Since, we were not given a situation on the triangle, so we assumed the line ED to be the angle bisector by ourselves to solve for x. If any other situation is given then take that, and do not assume anything.
Cross check your answer by substituting the value, in the above equation on angle bisector. If the ratio on both sides is the same, the value obtained is absolutely correct.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE





