Question

What is the value of the integral $\int_{0}^{\sqrt{2}}{\left[ {{x}^{2}} \right]dx}$ where [.] denotes the greatest integer function.
[a] $\sqrt{2}-1$
[b] $1-\sqrt{2}$
[c] $2\left( \sqrt{2}-1 \right)$
[d] $\sqrt{3}-1$

Answer 1

- Hint: Use the fact that if a
Complete step-by-step solution -

First fundamental theorem of Calculus:
According to the first fundamental theorem of calculus if f(x) is continuous in the interval (a,b) and a function F(x) satisfies F’(x) = f(x), then $\int_{a}^{b}{f\left( x \right)dx}=F\left( b \right)-F\left( a \right)$. We use the first fundamental theorem of calculus to find the above integral.
Let $I=\int_{0}^{\sqrt{2}}{{{x}^{2}}}$
In the interval $\left[ 0,\sqrt{2} \right]$, we have $0\le {{x}^{2}}\le 2$
Dividing into interval such that $0\le {{x}^{2}}\le 1$ and $1\le {{x}^{2}}\le 2$
Hence, we have $0\le x\le 1$ and $1\le x\le \sqrt{2}$
We know that if aTaking a = 0 , $b=\sqrt{2}$ and c = 1 and $f\left( x \right)=\left[ {{x}^{2}} \right]$, we get
Hence we have $\int_{0}^{\sqrt{2}}{\left[ {{x}^{2}} \right]dx}=\int_{0}^{1}{\left[ {{x}^{2}} \right]dx}+\int_{1}^{\sqrt{2}}{\left[ {{x}^{2}} \right]dx}$
Now we have that in the interval (0,1) $\left[ {{x}^{2}} \right]=0$ and in the interval $\left[ 1,\sqrt{2} \right]$, $\left[ {{x}^{2}} \right]=1$
Hence the above integral becomes
$I=\int_{0}^{1}{0dx}+\int_{1}^{\sqrt{2}}{1dx}$
Now we know that $\int{1dx}=x$
Hence from fundamental theorem of calculus, we have
$\int_{1}^{\sqrt{2}}{\left[ {{x}^{2}} \right]dx}=\int_{1}^{\sqrt{2}}{1dx}=\left. x \right|_{1}^{\sqrt{2}}=\sqrt{2}-1$
Hence $I=0+\sqrt{2}-1=\sqrt{2}-1$
Hence option [a] is correct.


Note: Finding area under the curve graphically.
Plotting the graph of $y={{x}^{2}}$
The graph of the function $y={{x}^{2}}$ is shown below

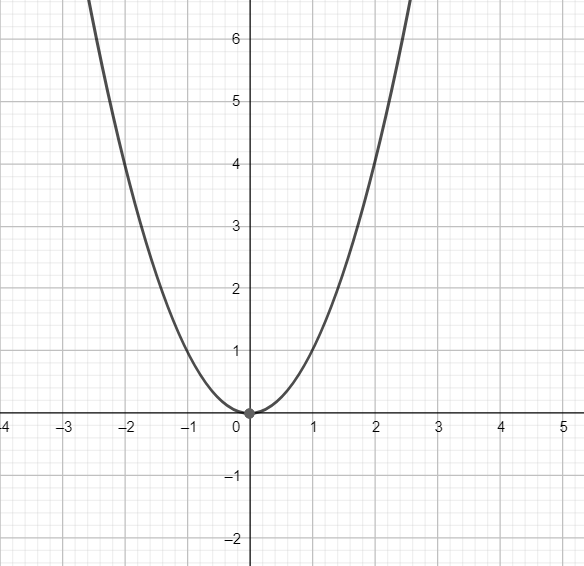
Plotting $y=\left[ {{x}^{2}} \right]$
As is evident from the graph of $y={{x}^{2}}$, the graph of $y=\left[ {{x}^{2}} \right]$ is shown below

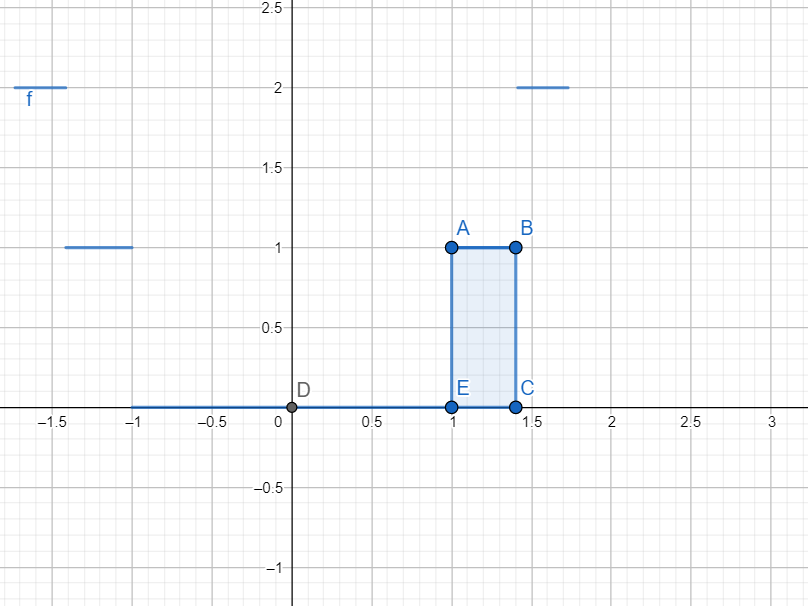
Hence $\int_{0}^{\sqrt{2}}{\left[ {{x}^{2}} \right]=}$ Area of ABCE = $\left( \sqrt{2}-1 \right)\left( 1 \right)=\sqrt{2}-1$, which is same as obtained above.