
What is the value of linear velocity? If \[\vec \omega = 3\hat i + 4\hat j + \hat k\] and \[\vec r = 5\hat i - 6\hat j + 6\hat k\]
Answer
569.7k+ views
Hint: When a body moves in the angular way i.e. circular motion and rotatory motion, with constant speed, it’s direction changes continuously so the angular velocity of body changes with respect to time, hence it has a linear velocity which is we are going to find. By remembering that it is a velocity not the speed because in uniform circular/rotational motion the speed remains constant. The linear and angular velocities both are vector quantities.
Formula used: Relation between linear velocity and angular velocity-
\[\vec v = \vec r \times \vec \omega \]
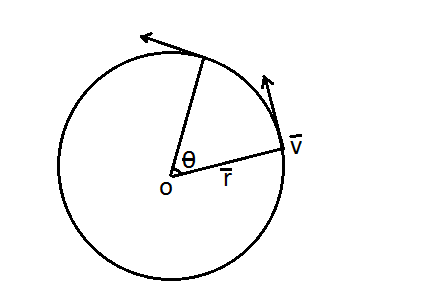
Where \[\vec v\] is linear velocity of body, \[\vec \omega \] is angular velocity of body, \[\vec r\] is the radius of Path.
Complete step by step solution:
The linear velocity of any rotating body is defined as the cross product of the angular velocity and the radius of path. In this question the angular velocity and the radius of path, in which the body is moving is given as –
\[\vec \omega = 3\hat i + 4\hat j + \hat k\]
\[\vec r = 5\hat i - 6\hat j + 6\hat k\]
\[\vec v = ?\]
We know from the relation of linear velocity and angular velocity
\[\vec v = \vec r \times \vec \omega \]
\[
\Rightarrow \vec v = (5\hat i - 6\hat j + 6\hat k) \times (3\hat i + 4\hat j + \hat k) \\
\Rightarrow \vec v = \left| {\begin{array}{*{20}{c}}
{\hat i}&{\hat j}&{\hat k} \\
5&{ - 6}&6 \\
3&4&1
\end{array}} \right| \\
\Rightarrow \vec v = \hat i\{ - 6 - 24\} - \hat j\{ 5 - 18\} + \hat k\{ 20 - ( - 18)\} \\
\Rightarrow \vec v = \hat i( - 6 - 24) - \hat j(5 - 18) + \hat k(20 + 18) \\
\Rightarrow \vec v = \hat i( - 30) - ( - 13)\hat j + 38\hat k \\
\Rightarrow \vec v = 30\hat i + 13\hat j + 38\hat k \\
\]
Hence, the linear velocity of the body is \[\vec v = 30\hat i + 13\hat j + 38\hat k\]
Additional Information: The magnitude of linear velocity is \[m/{s^2}\]and for a complete revolution the average velocity of any rotating body is always zero. And angular acceleration is also found by this velocity.
Angular velocity = the rate of change of angular displacement with respect to time is called angular velocity. And denoted by\[\vec \omega \].
Angular acceleration = the rate of change of angular velocity with respect to time is called angular acceleration. And denoted by\[\vec a\].
\[
\vec a = \dfrac{{{{\vec v}^2}}}{r} \\
\Rightarrow \vec a = \dfrac{{{r^2}{\omega ^2}}}{r} \\
\Rightarrow \vec a = r{\omega ^2} \\
\]
Angular acceleration is always changing with the change of direction.
Note:When we find the cross product of \[r\]and\[\omega \], \[\hat j\] is taken as negative. If angle is given in the problem than we can apply the formula \[\vec A \times \vec B = \left| A \right|\left| B \right|\sin \theta \]
Where \[\left| A \right|\]is magnitude of\[\vec A\] and \[\left| B \right|\] is the magnitude of\[\vec B\].
Formula used: Relation between linear velocity and angular velocity-
\[\vec v = \vec r \times \vec \omega \]
Where \[\vec v\] is linear velocity of body, \[\vec \omega \] is angular velocity of body, \[\vec r\] is the radius of Path.
Complete step by step solution:
The linear velocity of any rotating body is defined as the cross product of the angular velocity and the radius of path. In this question the angular velocity and the radius of path, in which the body is moving is given as –
\[\vec \omega = 3\hat i + 4\hat j + \hat k\]
\[\vec r = 5\hat i - 6\hat j + 6\hat k\]
\[\vec v = ?\]

We know from the relation of linear velocity and angular velocity
\[\vec v = \vec r \times \vec \omega \]
\[
\Rightarrow \vec v = (5\hat i - 6\hat j + 6\hat k) \times (3\hat i + 4\hat j + \hat k) \\
\Rightarrow \vec v = \left| {\begin{array}{*{20}{c}}
{\hat i}&{\hat j}&{\hat k} \\
5&{ - 6}&6 \\
3&4&1
\end{array}} \right| \\
\Rightarrow \vec v = \hat i\{ - 6 - 24\} - \hat j\{ 5 - 18\} + \hat k\{ 20 - ( - 18)\} \\
\Rightarrow \vec v = \hat i( - 6 - 24) - \hat j(5 - 18) + \hat k(20 + 18) \\
\Rightarrow \vec v = \hat i( - 30) - ( - 13)\hat j + 38\hat k \\
\Rightarrow \vec v = 30\hat i + 13\hat j + 38\hat k \\
\]
Hence, the linear velocity of the body is \[\vec v = 30\hat i + 13\hat j + 38\hat k\]
Additional Information: The magnitude of linear velocity is \[m/{s^2}\]and for a complete revolution the average velocity of any rotating body is always zero. And angular acceleration is also found by this velocity.
Angular velocity = the rate of change of angular displacement with respect to time is called angular velocity. And denoted by\[\vec \omega \].
Angular acceleration = the rate of change of angular velocity with respect to time is called angular acceleration. And denoted by\[\vec a\].
\[
\vec a = \dfrac{{{{\vec v}^2}}}{r} \\
\Rightarrow \vec a = \dfrac{{{r^2}{\omega ^2}}}{r} \\
\Rightarrow \vec a = r{\omega ^2} \\
\]
Angular acceleration is always changing with the change of direction.
Note:When we find the cross product of \[r\]and\[\omega \], \[\hat j\] is taken as negative. If angle is given in the problem than we can apply the formula \[\vec A \times \vec B = \left| A \right|\left| B \right|\sin \theta \]
Where \[\left| A \right|\]is magnitude of\[\vec A\] and \[\left| B \right|\] is the magnitude of\[\vec B\].
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




