
What is the value of $\cos {{20}^{\circ }}+\cos {{22}^{\circ }}+\cos {{158}^{\circ }}+\cos {{200}^{\circ }}+\cos {{300}^{\circ }}$?
Answer
598.8k+ views
Hint: We will use the formula, $\cos \left( {{180}^{\circ }}-\theta \right)=-\cos \theta $ and $\cos \left( {{180}^{\circ }}+\theta \right)=-\cos \theta $ to express $\cos \left( {{158}^{\circ }} \right)=\cos \left( {{180}^{\circ }}-{{22}^{\circ }} \right)=-\cos \left( {{22}^{\circ }} \right)$ and \[\cos \left( {{200}^{\circ }} \right)=\cos \left( {{180}^{\circ }}+{{20}^{\circ }} \right)=-\cos \left( {{20}^{\circ }} \right)\]. We will also express $\cos \left( {{300}^{\circ }} \right)=\cos \left( {{360}^{\circ }}-{{60}^{\circ }} \right)=\cos \left( {{60}^{\circ }} \right)$. Finally we will arrange the obtained trigonometric terms and find the value of the whole expression.
Complete step-by-step answer:
It is given in the question that we have to find the value of $\cos {{20}^{\circ }}+\cos {{22}^{\circ }}+\cos {{158}^{\circ }}+\cos {{200}^{\circ }}+\cos {{300}^{\circ }}$. We know that the value of $\cos \theta $ is positive in the first and the fourth quadrant. Whereas $\cos \theta $ is negative in the second and the third quadrant.
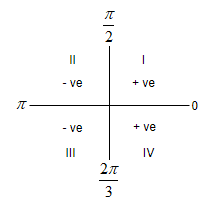
Now, we know that $\cos \left( {{180}^{\circ }}-\theta \right)=-\cos \theta $ and $\cos \left( {{180}^{\circ }}+\theta \right)=-\cos \theta $. So, by using this concept, we can write, $\cos \left( {{158}^{\circ }} \right)$ as $\cos \left( {{180}^{\circ }}-{{22}^{\circ }} \right)$ which is equal to $-\cos \left( {{22}^{\circ }} \right)$. Thus, $\cos \left( {{158}^{\circ }} \right)$ can be expressed as $-\cos \left( {{22}^{\circ }} \right)$.
Similarly, \[\cos \left( {{200}^{\circ }} \right)\] can be written as \[\cos \left( {{180}^{\circ }}+{{20}^{\circ }} \right)\] which is equal to \[-\cos \left( {{20}^{\circ }} \right)\].
Thus, \[\cos \left( {{200}^{\circ }} \right)\] can be expressed as \[-\cos \left( {{20}^{\circ }} \right)\].
Also, we can write \[\cos \left( {{300}^{\circ }} \right)\] as \[\cos \left( {{360}^{\circ }}+{{300}^{\circ }} \right)\] which is equal to \[\cos \left( {{60}^{\circ }} \right)\] because cos is positive in the first and the fourth quadrant.
Thus, \[\cos \left( {{300}^{\circ }} \right)\] can be expressed as \[\cos \left( {{60}^{\circ }} \right)\].
Now, on putting the new values of $\cos \left( {{158}^{\circ }} \right),\cos \left( {{200}^{\circ }} \right),\cos \left( {{300}^{\circ }} \right)$ in the expression, $\cos {{20}^{\circ }}+\cos {{22}^{\circ }}+\cos {{158}^{\circ }}+\cos {{200}^{\circ }}+\cos {{300}^{\circ }}$, we will get as follows,
$\cos {{20}^{\circ }}+\cos {{22}^{\circ }}-\cos {{22}^{\circ }}-\cos {{20}^{\circ }}+\cos {{60}^{\circ }}$
On cancelling the similar terms, we will get,
\[\cos {{60}^{\circ }}\]
Now, we know that \[\cos {{60}^{\circ }}=\dfrac{1}{2}\], so we will get,
\[\cos {{60}^{\circ }}=\dfrac{1}{2}\]
Therefore, the value of the expression, that is, $\cos {{20}^{\circ }}+\cos {{22}^{\circ }}+\cos {{158}^{\circ }}+\cos {{200}^{\circ }}+\cos {{300}^{\circ }}$ is equal to $\dfrac{1}{2}$.
Note: It is observed that most of the students make mistake in taking the sign while writing $\cos \left( {{360}^{\circ }}-{{60}^{\circ }} \right)=\cos \left( {{60}^{\circ }} \right)$. They may write it as $\cos \left( {{360}^{\circ }}-{{60}^{\circ }} \right)=-\cos \left( {{60}^{\circ }} \right)$, and thus they will get, \[-\cos {{60}^{\circ }}=-\dfrac{1}{2}\] and we know that \[-\dfrac{1}{2}\] is not the correct answer. Thus it is recommended that the students take proper care of signs while solving the question.
Complete step-by-step answer:
It is given in the question that we have to find the value of $\cos {{20}^{\circ }}+\cos {{22}^{\circ }}+\cos {{158}^{\circ }}+\cos {{200}^{\circ }}+\cos {{300}^{\circ }}$. We know that the value of $\cos \theta $ is positive in the first and the fourth quadrant. Whereas $\cos \theta $ is negative in the second and the third quadrant.
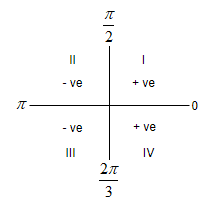
Now, we know that $\cos \left( {{180}^{\circ }}-\theta \right)=-\cos \theta $ and $\cos \left( {{180}^{\circ }}+\theta \right)=-\cos \theta $. So, by using this concept, we can write, $\cos \left( {{158}^{\circ }} \right)$ as $\cos \left( {{180}^{\circ }}-{{22}^{\circ }} \right)$ which is equal to $-\cos \left( {{22}^{\circ }} \right)$. Thus, $\cos \left( {{158}^{\circ }} \right)$ can be expressed as $-\cos \left( {{22}^{\circ }} \right)$.
Similarly, \[\cos \left( {{200}^{\circ }} \right)\] can be written as \[\cos \left( {{180}^{\circ }}+{{20}^{\circ }} \right)\] which is equal to \[-\cos \left( {{20}^{\circ }} \right)\].
Thus, \[\cos \left( {{200}^{\circ }} \right)\] can be expressed as \[-\cos \left( {{20}^{\circ }} \right)\].
Also, we can write \[\cos \left( {{300}^{\circ }} \right)\] as \[\cos \left( {{360}^{\circ }}+{{300}^{\circ }} \right)\] which is equal to \[\cos \left( {{60}^{\circ }} \right)\] because cos is positive in the first and the fourth quadrant.
Thus, \[\cos \left( {{300}^{\circ }} \right)\] can be expressed as \[\cos \left( {{60}^{\circ }} \right)\].
Now, on putting the new values of $\cos \left( {{158}^{\circ }} \right),\cos \left( {{200}^{\circ }} \right),\cos \left( {{300}^{\circ }} \right)$ in the expression, $\cos {{20}^{\circ }}+\cos {{22}^{\circ }}+\cos {{158}^{\circ }}+\cos {{200}^{\circ }}+\cos {{300}^{\circ }}$, we will get as follows,
$\cos {{20}^{\circ }}+\cos {{22}^{\circ }}-\cos {{22}^{\circ }}-\cos {{20}^{\circ }}+\cos {{60}^{\circ }}$
On cancelling the similar terms, we will get,
\[\cos {{60}^{\circ }}\]
Now, we know that \[\cos {{60}^{\circ }}=\dfrac{1}{2}\], so we will get,
\[\cos {{60}^{\circ }}=\dfrac{1}{2}\]
Therefore, the value of the expression, that is, $\cos {{20}^{\circ }}+\cos {{22}^{\circ }}+\cos {{158}^{\circ }}+\cos {{200}^{\circ }}+\cos {{300}^{\circ }}$ is equal to $\dfrac{1}{2}$.
Note: It is observed that most of the students make mistake in taking the sign while writing $\cos \left( {{360}^{\circ }}-{{60}^{\circ }} \right)=\cos \left( {{60}^{\circ }} \right)$. They may write it as $\cos \left( {{360}^{\circ }}-{{60}^{\circ }} \right)=-\cos \left( {{60}^{\circ }} \right)$, and thus they will get, \[-\cos {{60}^{\circ }}=-\dfrac{1}{2}\] and we know that \[-\dfrac{1}{2}\] is not the correct answer. Thus it is recommended that the students take proper care of signs while solving the question.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

10 examples of friction in our daily life




