
Using the Venn diagram shows that $(A - B)$,$(A \cap B)$ and $(B - A)$ are disjoint sets, taking $A = \left\{ {2,4,6,8,10,\left. {12} \right\}} \right.$and $B = \left\{ {3,6,9,12,\left. {15} \right\}} \right.$
Answer
469.5k+ views
Hint: First, we have to define what the terms we need to solve the problem are.
Since disjoint means the common values of the two or more than two sets are empty (no values occur)
It was also known as$A \cap B = \phi $. Also, there are two sets given, the set of A has the multiple of two and the set of all B has the multiple of three.
Complete step by step answer:
Let from the given two sets $A = \left\{ {2,4,6,8,10,\left. {12} \right\}} \right.$and $B = \left\{ {3,6,9,12,\left. {15} \right\}} \right.$ first, we need to find the required sets like $(A - B)$ ,$(A \cap B)$and$(B - A)$
First, we will find $(A - B)$(set of A subtracts set of B) which is the subtraction operator into the sets;
It refers to $A = \left\{ {2,4,6,8,10,\left. {12} \right\}} \right.$subtract (common elements comparing to B will be eliminated) the $B = \left\{ {3,6,9,12,\left. {15} \right\}} \right.$ then $(A - B) = \left\{ {2,4,6,8,\left. {10} \right\}} \right.$since A and B have $12$as the common number so that element from A only eliminated;
Similarly in the same way we can prove; $(B - A)$(the common elements of B only need to be eliminated)
Hence $(B - A) = \left\{ {3,9,\left. {15} \right\}} \right.$(since comparing B and A the two common elements are $6$,$12$)
Now for $(A \cap B)$which is the intersection of the two sets; only the common numbers will occur in this set. Hence $(A \cap B) = \left\{ {6,\left. {12} \right\}} \right.$(six and twelve are the only two elements that occur in this set)
Thus, we have all the set values $(A - B) = \left\{ {2,4,6,8,\left. {10} \right\}} \right.$$(B - A) = \left\{ {3,9,\left. {15} \right\}} \right.$$(A \cap B) = \left\{ {6,\left. {12} \right\}} \right.$ Now we will check the intersection of all sets; if it occurs empty then it is disjoint set or not disjoint
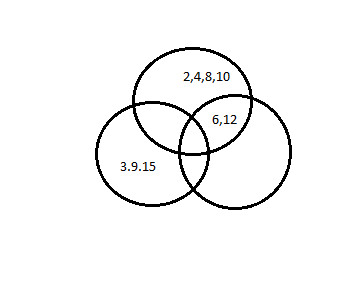
Thus, we see there are no common points or numbers for the three sets $(A - B)$,$(A \cap B)$ and $(B - A)$ hence it is a disjoint set; as we said the intersection of the sets is empty.
Note:
Since $(A - B)$ means the set of all elements of set, A has no common points compared to set B and $(B - A)$ is as similar. Distinct means difference set and disjoint means intersection empty set.
Also empty is said to be a set in set theory.
Since disjoint means the common values of the two or more than two sets are empty (no values occur)
It was also known as$A \cap B = \phi $. Also, there are two sets given, the set of A has the multiple of two and the set of all B has the multiple of three.
Complete step by step answer:
Let from the given two sets $A = \left\{ {2,4,6,8,10,\left. {12} \right\}} \right.$and $B = \left\{ {3,6,9,12,\left. {15} \right\}} \right.$ first, we need to find the required sets like $(A - B)$ ,$(A \cap B)$and$(B - A)$
First, we will find $(A - B)$(set of A subtracts set of B) which is the subtraction operator into the sets;
It refers to $A = \left\{ {2,4,6,8,10,\left. {12} \right\}} \right.$subtract (common elements comparing to B will be eliminated) the $B = \left\{ {3,6,9,12,\left. {15} \right\}} \right.$ then $(A - B) = \left\{ {2,4,6,8,\left. {10} \right\}} \right.$since A and B have $12$as the common number so that element from A only eliminated;
Similarly in the same way we can prove; $(B - A)$(the common elements of B only need to be eliminated)
Hence $(B - A) = \left\{ {3,9,\left. {15} \right\}} \right.$(since comparing B and A the two common elements are $6$,$12$)
Now for $(A \cap B)$which is the intersection of the two sets; only the common numbers will occur in this set. Hence $(A \cap B) = \left\{ {6,\left. {12} \right\}} \right.$(six and twelve are the only two elements that occur in this set)
Thus, we have all the set values $(A - B) = \left\{ {2,4,6,8,\left. {10} \right\}} \right.$$(B - A) = \left\{ {3,9,\left. {15} \right\}} \right.$$(A \cap B) = \left\{ {6,\left. {12} \right\}} \right.$ Now we will check the intersection of all sets; if it occurs empty then it is disjoint set or not disjoint
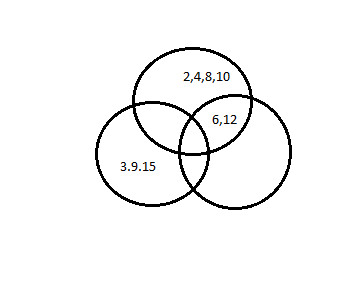
Thus, we see there are no common points or numbers for the three sets $(A - B)$,$(A \cap B)$ and $(B - A)$ hence it is a disjoint set; as we said the intersection of the sets is empty.
Note:
Since $(A - B)$ means the set of all elements of set, A has no common points compared to set B and $(B - A)$ is as similar. Distinct means difference set and disjoint means intersection empty set.
Also empty is said to be a set in set theory.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




