Question

Using the numbers from 9 to 17 construct a \[{\text{3}} \times {\text{3}}\] magic square. What is the magic sum here? What relation is there between the magic sum and the number in the central cell?

Answer 1

Hint: See here we have 9 numbers in total. We have to arrange them in order that their sum is something magical. We will take 13 as the number in the central cell because remaining numbers if paired and arranged will give 39 as the sum. The only trick is the way we arrange them.so let's play!

Complete step-by-step answer:
We have numbers from 9 to 17. That is 9,10,11,12,13,14,15,16,17.
Now we have some pairs like \[{\text{9 + 13 + 17,10 + 13 + 16,11 + 13 + 15,12 + 13 + 14}}\] that add 39 as the sum.
But these are only four and in a \[{\text{3}} \times {\text{3}}\] magic square we have 3 horizontal as well as 3 vertical lines to be filled.
So we will arrange these numbers to get the perfect combination.
 

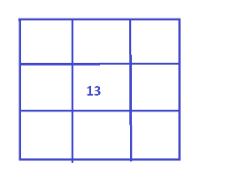
This is the central cell number and is fixed.
Now we will start from the left most corner and the very first trio of our numbers.

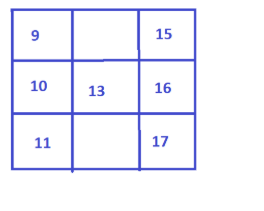
This will make the conditions to be satisfied but as we input the lats trio,

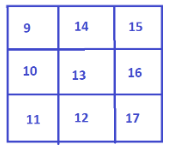
But this disturbs the previous arrangement. So we found some more trios,
\[9 + 14 + 16,10 + 12 + 17,11 + 13 + 15,\]
Now we can arrange the numbers as,

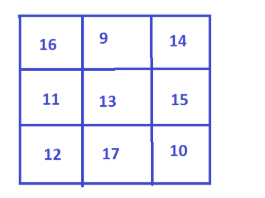
This arrangement can be observed to be the magic square with magic sum inside

Note: Finding the central cell number is not that difficult but arranging the numbers can be quite difficult. We need to find the relation between the numbers and then we can put the numbers in the correct place.