Question

Using section formula show that the points $A\left( 2,-3,4 \right),B\left( -1,2,1 \right)$ and $C\left( 0,\dfrac{1}{3},2 \right)$ are collinear.

Answer 1

Hint: Points $A,B,C$ are collinear if point $C$ divides the line $AB$ in some ratio. This ratio can be found out using section formula.

Complete step-by-step answer:
Before proceeding with the question, we must know the section formula. Let us consider a line $AB$ with a point $C$ lying on it. Let us assume that point $C$ is dividing this line $AB$ in ratio of $m:n$.

If the coordinates of $A$ is $\left( x',y',z' \right)$ and the coordinates of $B$ is $\left( x'',y'',z'' \right)$, then, from the section formula, the coordinates of $C$ are,
$\left( \dfrac{mx''+nx'}{m+n},\dfrac{my''+ny'}{m+n},\dfrac{mz''+nz'}{m+n} \right)................\left( 1 \right)$
In this question, we have to prove that point $A\left( 2,-3,4 \right),B\left( -1,2,1 \right)$ and $C\left( 0,\dfrac{1}{3},2 \right)$ are collinear. Points $A,B,C$ can be said to be collinear if point $C$ divides the line $AB$ in some ratio. Let us assume that point $C$ divides the line $AB$ in a ratio $k:1$.

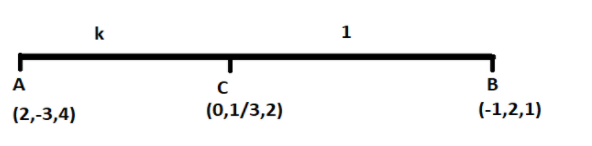
From the section formula, we can find the value of $k$. Using section formula in equation $\left( 1 \right)$, finding the $x,y,z$ coordinates of the point $C$individually, we get,
$i)$ $x$ coordinate of point $C$ = $\left( \dfrac{\left( k \right)\left( -1 \right)+\left( 1 \right)\left( 2 \right)}{k+1} \right)$
$\begin{align}
  & \Rightarrow 0=\dfrac{-k+2}{k+1} \\
 & \Rightarrow -k+2=0 \\
 & \Rightarrow k=2 \\
\end{align}$
$ii)$ $y$ coordinate of point $C$ =$\left( \dfrac{k\left( 2 \right)+\left( 1 \right)\left( -3 \right)}{k+1} \right)$
$\begin{align}
  & \Rightarrow \dfrac{1}{3}=\dfrac{2k-3}{k+1} \\
 & \Rightarrow k+1=6k-9 \\
 & \Rightarrow 5k=10 \\
 & \Rightarrow k=2 \\
\end{align}$
$iii)$ $z$ coordinate of point $C$ = $\left( \dfrac{k\left( 1 \right)+\left( 1 \right)\left( 4 \right)}{k+1} \right)$
$\begin{align}
  & \Rightarrow 2=\dfrac{k+4}{k+1} \\
 & \Rightarrow 2k+2=k+4 \\
 & \Rightarrow k=2 \\
\end{align}$
Using section formula, we calculated the value of $k$ from $x,y,z$ coordinates individually in $\left( i \right),\left( ii \right),\left( iii \right)$. In every of the above case $\left( i \right),\left( ii \right),\left( iii \right)$, we get the same value of $k$. Since we got a unique value of $k$ in all these cases, we can say that point $C$ divides the line $AB$ in ratio of $2:1$. This also means that point $C$ lies on the line $AB$. Hence, we can say that points $A,B,C$ are collinear.
Hence, we can say that $A,B,C$ are collinear.

Note: If we get different values of $k$ from equation obtained in $x,y,z$ coordinates in the section formula, we can say that the point $C$ does not lie on the line $AB$ and hence, we can say that $A,B,C$ are not collinear.