
Using MOT, compare $O_{2}^{+}\,and\,O_{2}^{-}$ species and choose the incorrect option.
(A)- $O_{2}^{+}$ have higher bond order than $O_{2}^{-}$
(B)- $O_{2}^{-}$is less stable
(C)- $O_{2}^{+}$is diamagnetic while $O_{2}^{-}$ is paramagnetic
(D)- Both $O_{2}^{+}$and $O_{2}^{-}$ are paramagnetic
Answer
577.5k+ views
Hint: In the given species, using MOT we will determine the accommodation of the electrons in the molecular orbitals which will further help in determining the bond order, stability, and magnetic nature of the molecule.
Complete step by step solution:
In the oxygen atom, with Z = 8, it has electronic configuration $1{{s}^{2}}2{{s}^{2}}2{{p}^{4}}$. Then the total number of electrons in ${{O}_{2}}$ is 16. In the $O_{2}^{+}$ form, deficient of one electron, it has a total of 15 electrons and with one extra electron the $O_{2}^{-}$ form has 17 electrons.
The atoms combine together to form the molecule, in which the electrons are now accommodated in the molecular orbitals. So, the electronic configuration of the species is as follows:
$O_{2}^{+}={{(\sigma 1s)}^{2}}{{({{\sigma }^{*}}1s)}^{2}}{{(\sigma 2s)}^{2}}{{({{\sigma }^{*}}2s)}^{2}}{{(\sigma 2{{p}_{z}})}^{2}}{{(\pi 2{{p}_{x}})}^{2}}={{(\pi 2{{p}_{y}})}^{2}}{{({{\pi }^{*}}2{{p}_{x}})}^{1}}$
$O_{2}^{+}={{(\sigma 1s)}^{2}}{{({{\sigma }^{*}}1s)}^{2}}{{(\sigma 2s)}^{2}}{{({{\sigma }^{*}}2s)}^{2}}{{(\sigma 2{{p}_{z}})}^{2}}{{(\pi 2{{p}_{x}})}^{2}}={{(\pi 2{{p}_{y}})}^{2}}{{({{\pi }^{*}}2{{p}_{x}})}^{2}}{{({{\pi }^{*}}2{{p}_{y}})}^{1}}$
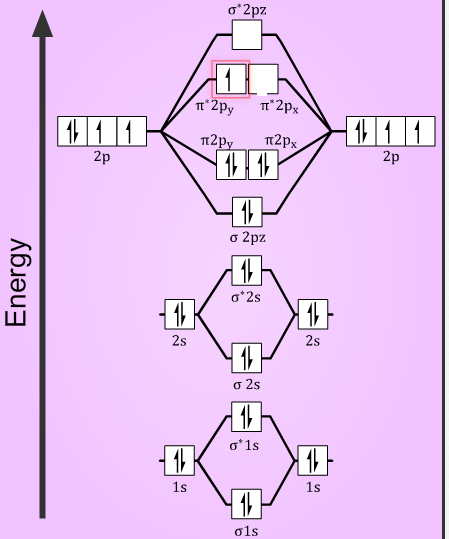
Then, the bond order of the species will be now determined using the number of electrons the bonding and the antibonding orbitals, from the formula:
$\text{Bond}\,\text{order = }\dfrac{\text{1}}{\text{2}}\text{ (no}\text{.}\,\text{of}\,\text{electrons}\,\,\text{in}\,\,\text{bonding}\,\text{orbitals - no}\text{.}\,\text{of}\,\text{electrons}\,\text{in}\,\text{anti-bonding}\,\text{orbitals)}$
So, in $O_{2}^{+}$ molecules with 10 electrons in bonding orbitals and 5 electrons in antibonding orbitals. The bond order is $=\dfrac{(10-5)}{2}=2.5$
Similarly, in $O_{2}^{-}$ molecules, with 10 electrons in bonding orbitals and 7 electrons in antibonding orbitals. The bond order is $=\dfrac{(10-7)}{2}=1.5$
Thus, the bond order of $O_{2}^{+}$ is higher than $O_{2}^{-}$ molecule.
Now, the stability of the molecule is determined by the number of electrons in the antibonding orbital. More the number of electrons in the antibonding orbitals, more is the instability of the molecule. So, the $O_{2}^{-}$ with greater number of electrons in the antibonding orbitals compared to $O_{2}^{+}$ . It is less stable.
Also, with the number of unpaired electrons in the molecule, the magnetic nature can be determined. As from the electronic configuration it is seen that, both the species have one unpaired electron in their anti-bonding orbital. Thus, making them paramagnetic in nature.
Therefore, the incorrect statement for the given species will be option (C)- $O_{2}^{+}$is diamagnetic while $O_{2}^{-}$ is paramagnetic.
Note: The energy of the bonding orbital is lower than the antibonding orbitals in the molecule. And the filling of electrons in the molecular orbitals also follows the Aufbau principle, Pauli’s exclusion principle and the Hund’s rule.
Complete step by step solution:
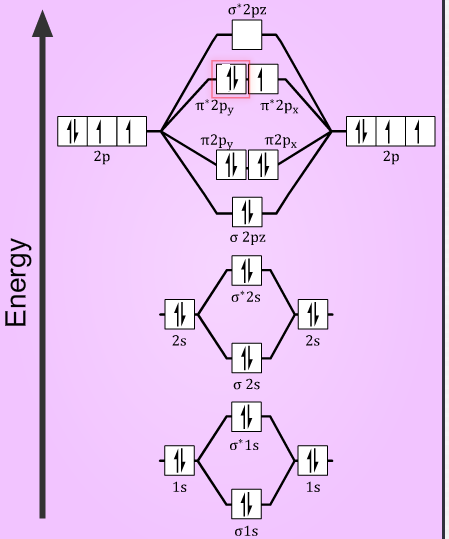
In the oxygen atom, with Z = 8, it has electronic configuration $1{{s}^{2}}2{{s}^{2}}2{{p}^{4}}$. Then the total number of electrons in ${{O}_{2}}$ is 16. In the $O_{2}^{+}$ form, deficient of one electron, it has a total of 15 electrons and with one extra electron the $O_{2}^{-}$ form has 17 electrons.
The atoms combine together to form the molecule, in which the electrons are now accommodated in the molecular orbitals. So, the electronic configuration of the species is as follows:
$O_{2}^{+}={{(\sigma 1s)}^{2}}{{({{\sigma }^{*}}1s)}^{2}}{{(\sigma 2s)}^{2}}{{({{\sigma }^{*}}2s)}^{2}}{{(\sigma 2{{p}_{z}})}^{2}}{{(\pi 2{{p}_{x}})}^{2}}={{(\pi 2{{p}_{y}})}^{2}}{{({{\pi }^{*}}2{{p}_{x}})}^{1}}$
$O_{2}^{+}={{(\sigma 1s)}^{2}}{{({{\sigma }^{*}}1s)}^{2}}{{(\sigma 2s)}^{2}}{{({{\sigma }^{*}}2s)}^{2}}{{(\sigma 2{{p}_{z}})}^{2}}{{(\pi 2{{p}_{x}})}^{2}}={{(\pi 2{{p}_{y}})}^{2}}{{({{\pi }^{*}}2{{p}_{x}})}^{2}}{{({{\pi }^{*}}2{{p}_{y}})}^{1}}$


Then, the bond order of the species will be now determined using the number of electrons the bonding and the antibonding orbitals, from the formula:
$\text{Bond}\,\text{order = }\dfrac{\text{1}}{\text{2}}\text{ (no}\text{.}\,\text{of}\,\text{electrons}\,\,\text{in}\,\,\text{bonding}\,\text{orbitals - no}\text{.}\,\text{of}\,\text{electrons}\,\text{in}\,\text{anti-bonding}\,\text{orbitals)}$
So, in $O_{2}^{+}$ molecules with 10 electrons in bonding orbitals and 5 electrons in antibonding orbitals. The bond order is $=\dfrac{(10-5)}{2}=2.5$
Similarly, in $O_{2}^{-}$ molecules, with 10 electrons in bonding orbitals and 7 electrons in antibonding orbitals. The bond order is $=\dfrac{(10-7)}{2}=1.5$
Thus, the bond order of $O_{2}^{+}$ is higher than $O_{2}^{-}$ molecule.
Now, the stability of the molecule is determined by the number of electrons in the antibonding orbital. More the number of electrons in the antibonding orbitals, more is the instability of the molecule. So, the $O_{2}^{-}$ with greater number of electrons in the antibonding orbitals compared to $O_{2}^{+}$ . It is less stable.
Also, with the number of unpaired electrons in the molecule, the magnetic nature can be determined. As from the electronic configuration it is seen that, both the species have one unpaired electron in their anti-bonding orbital. Thus, making them paramagnetic in nature.
Therefore, the incorrect statement for the given species will be option (C)- $O_{2}^{+}$is diamagnetic while $O_{2}^{-}$ is paramagnetic.
Note: The energy of the bonding orbital is lower than the antibonding orbitals in the molecule. And the filling of electrons in the molecular orbitals also follows the Aufbau principle, Pauli’s exclusion principle and the Hund’s rule.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




