Question

Using MO theory, predict which of the following species has the shortest bond length?
(A) ${{O}_{2}}^{2+}$
(B) ${{O}_{2}}^{+}$
(C) ${{O}_{2}}^{-}$
(D) ${{O}_{2}}^{2-}$

Answer 1

Hint: The Molecular Orbital Theory (MOT) explains the formation of the molecule in a better way than Valence Bond Theory (VBT). The bond order calculations are feasible using MOT thus, the bond length is calculated when we know bond order of molecules.

Complete step by step solution:
Before solving the illustration given let us see about the VBT, MOT, bond order and bond length relations. MOT and VBT are the foundational theories of quantum chemistry. The VBT gives a more understandable pictorial representation of molecules but, MOT explains the molecular formation in a better way. MOT describes the electronic structure of molecules using quantum mechanics. According to MOT, the atomic orbitals of comparable energy undergo overlap and give the formation of the same number of molecular orbitals.
Addition of atomic orbitals- The atomic orbitals with the same sign combine to give bonding molecular orbitals. In the molecular orbital, the region between the two nuclei is the place where there is overlap of individual orbitals. Hence, there is greater probability of electron density in this region. MOT uses a linear combination of atomic orbitals strategy to represent molecular orbitals resulting from bonds between atoms. These are bonding, anti-bonding and non-bonding.
-Let us see for ${{O}_{2}}$ molecule,

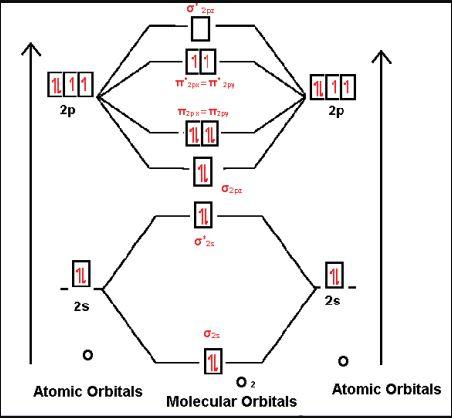
Molecular orbital electronic configuration is given by, MOEC = $KK{{\left( \sigma 2s \right)}^{2}}{{\left( {{\sigma }^{*}}2s \right)}^{2}}{{\left( \sigma 2{{p}_{z}} \right)}^{2}}\left[ {{\left( \pi 2{{p}_{x}} \right)}^{2}}={{\left( \pi 2{{p}_{y}} \right)}^{2}} \right]\left[ {{\left( {{\pi }^{*}}2{{p}_{x}} \right)}^{1}}={{\left( {{\pi }^{*}}2{{p}_{y}} \right)}^{1}} \right]$
-where, KK denotes ${{\left( \sigma 1s \right)}^{2}}{{\left( {{\sigma }^{*}}1s \right)}^{2}}$
-Bonding orbitals are $\sigma 2s,\sigma 2{{p}_{z}},\pi 2{{p}_{x}},\pi 2{{p}_{y}}$
-Anti-bonding orbitals are ${{\sigma }^{*}}2s,{{\sigma }^{*}}2{{p}_{z}},{{\pi }^{*}}2{{p}_{x}},{{\pi }^{*}}2{{p}_{y}}$
-Therefore, Bond order = $\dfrac{{{N}_{b}}-{{N}_{a}}}{2}$
-Here, ${{N}_{b}}$ denotes number of electrons in bonding molecular orbitals
-${{N}_{a}}$ denotes number of electrons in antibonding molecular orbitals
-So, Bond order of ${{O}_{2}}$ = $\dfrac{8-4}{2}=2$
-Fact- If an electron is removed from a stable atom to give cation, the electron is removed from the anti-bonding molecular orbital and vice versa.
-Thus, Bond order of ${{O}_{2}}^{2+}$= $\dfrac{8-2}{2}=3$
-Bond order of ${{O}_{2}}^{+}$= $\dfrac{8-3}{2}=2\dfrac{1}{2}$
-Bond order of ${{O}_{2}}^{-}$= $\dfrac{8-5}{2}=1\dfrac{1}{2}$
-Bond order of ${{O}_{2}}^{2-}$= $\dfrac{8-6}{2}=1$
-Now, Bond order is inversely proportional to Bond length, as higher the Bond order stronger will be the pull between two atoms combining with each other. Thus, shorter will be the Bond length. \[bond-order\propto \dfrac{1}{bond-length}\]. As ${{O}_{2}}^{2+}$ has the highest bond order, bond length will be small.

Therefore, option (A) is correct.

Note: The bonding MO has lower energy and hence greater stability whereas, anti-bonding MO has more energy and hence lesser stability. That is why, electrons will be added or removed from antibonding orbitals first.