
Using a table of values, graph a linear equation, $ y = - 2x + 5 $ .
Answer
543.9k+ views
Hint: In these types of questions, we have to make a graph by using a table of values of the given linear equation by finding the values of x and y and then plotting it on a graph and after plotting, we have to join the points. The graph of a linear equation is of a straight line.
Complete step by step solution:
The graph should be made by using a table of values. So, firstly we need to make a table and the table consists of three columns.
X-axis
$ y = - 2x + 5 $
Y-axis
Part (1)- X-axis- In this column, we will assume the values for x.
Part (2)- $ y = - 2x + 5 $ - In this column, we will substitute the value of x in this equation and solve for y.
Part (3)- Y-axis- In this column, we will write the values obtained from the given equation.
Now, we have the points i.e, $ \left( { - 2,9} \right),\left( { - 1,7} \right),\left( {0,5} \right),\left( {1,3} \right),\left( {2,1} \right) $ . Now, we will plot the graph with the help of the points.
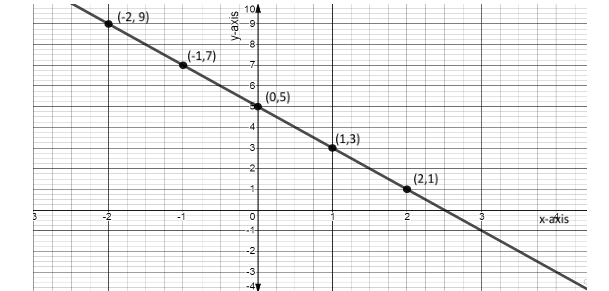
Note: This graph can also be made by the equation $ y = mx + b $ , where m is the slope, b is the y- intercept. Now, the above equation $ y = - 2x + 5 $ is similar to the equation $ y = mx + b $ and we can find from the equation that, here, $ m = - 2 $ and b will become $ 5 $ . As b is y- intercept, then one point we find is $ \left( {0,5} \right) $ and we know that, the slope is $ - 2 $ , and slope can also be written as,
Slope $ = \dfrac{{rise}}{{run}} $ ,
And the slope is $ - 2 $ , so, from the point $ \left( {0,5} \right) $ , we go two steps downward and one step right. Now, connect these two lines and then, we get a straight line.
Complete step by step solution:
The graph should be made by using a table of values. So, firstly we need to make a table and the table consists of three columns.
X-axis
$ y = - 2x + 5 $
Y-axis
Part (1)- X-axis- In this column, we will assume the values for x.
Part (2)- $ y = - 2x + 5 $ - In this column, we will substitute the value of x in this equation and solve for y.
Part (3)- Y-axis- In this column, we will write the values obtained from the given equation.
| x-axis | $ y = - 2x + 5 $ | y-axis |
| $ - 2 $ | $ y = - 2\left( { - 2} \right) + 5 = 4 + 5 = 9 $ | $ 9 $ |
| $ - 1 $ | $ y = - 2\left( { - 1} \right) + 5 = 2 + 5 = 7 $ | $ 7 $ |
| $ 0 $ | $ y = - 2\left( 0 \right) + 5 $ | $ 5 $ |
| $ 1 $ | $ y = - 2\left( 1 \right) + 5 = - 2 + 5 = 3 $ | $ 3 $ |
| $ 2 $ | $ y = - 2\left( 2 \right) + 5 = - 4 + 5 = 1 $ | $ 1 $ |
Now, we have the points i.e, $ \left( { - 2,9} \right),\left( { - 1,7} \right),\left( {0,5} \right),\left( {1,3} \right),\left( {2,1} \right) $ . Now, we will plot the graph with the help of the points.

Note: This graph can also be made by the equation $ y = mx + b $ , where m is the slope, b is the y- intercept. Now, the above equation $ y = - 2x + 5 $ is similar to the equation $ y = mx + b $ and we can find from the equation that, here, $ m = - 2 $ and b will become $ 5 $ . As b is y- intercept, then one point we find is $ \left( {0,5} \right) $ and we know that, the slope is $ - 2 $ , and slope can also be written as,
Slope $ = \dfrac{{rise}}{{run}} $ ,
And the slope is $ - 2 $ , so, from the point $ \left( {0,5} \right) $ , we go two steps downward and one step right. Now, connect these two lines and then, we get a straight line.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Find the mode and median of the data 13 16 12 14 1-class-9-maths-CBSE

What were the main changes brought about by the Bolsheviks class 9 social science CBSE

What is the theme or message of the poem The road not class 9 english CBSE

What are the major achievements of the UNO class 9 social science CBSE

Explain the importance of pH in everyday life class 9 chemistry CBSE

Differentiate between parenchyma collenchyma and sclerenchyma class 9 biology CBSE




