
Using a ruler and compass only.
(i) Construct a
AB = 3.5 cm, BC = 6 cm and
(ii) In the same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
(iii) Measure
Answer
502.2k+ views
Hint: In this problem, we are to find the figure with given instructions and also to find an angle. So, to start with we will draw the base which is of 6 cm and following that we will draw the angle of 120 degrees. Now, considering BC as a diameter we will draw a circle using the bisector. Now, we draw the angle bisector of the angle ABC and thus we get the equidistant points.
Complete step-by-step solution:
According to the question, we are to draw a triangle with the given conditions.
We will start with drawing a line segment BC which is equal to 6 cm.

Now, it is also said that,
So, we get,
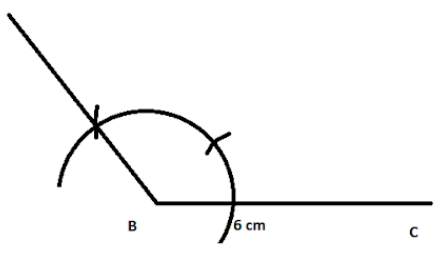
Again, it is said, AB = 3.5 cm,

Joining AB and AC will give us our desired triangle.
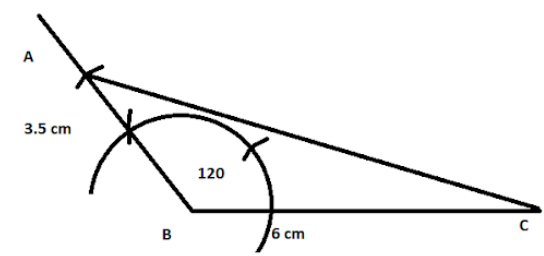
Now, for the second part,
We will start with drawing a bisector of BC.
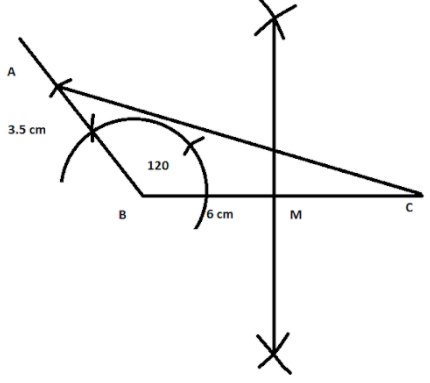
Now, to complete the circle,
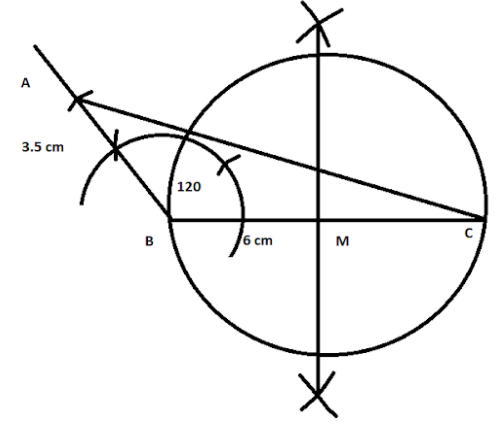
Again, we are to find a point on the circle which is equidistant from AB and BC.
So, we draw a bisector of the angle
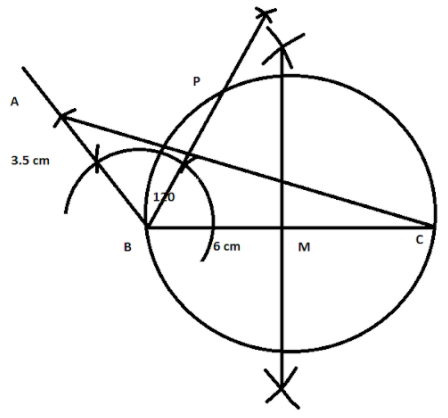
Joining C and P and measuring the angle we get,
Note: In this problem, we are to measure the angle we get in the last step. Sometimes, it might be the case that once we get the figure and we try to measure the angle, we will get the angles are not in whole numbers or in integers all the time. Then, we will try to consider it as a calculation problem and we will choose the nearest integer to get the solution.
Complete step-by-step solution:
According to the question, we are to draw a triangle with the given conditions.
We will start with drawing a line segment BC which is equal to 6 cm.

Now, it is also said that,
So, we get,

Again, it is said, AB = 3.5 cm,

Joining AB and AC will give us our desired triangle.

Now, for the second part,
We will start with drawing a bisector of BC.

Now, to complete the circle,

Again, we are to find a point on the circle which is equidistant from AB and BC.
So, we draw a bisector of the angle

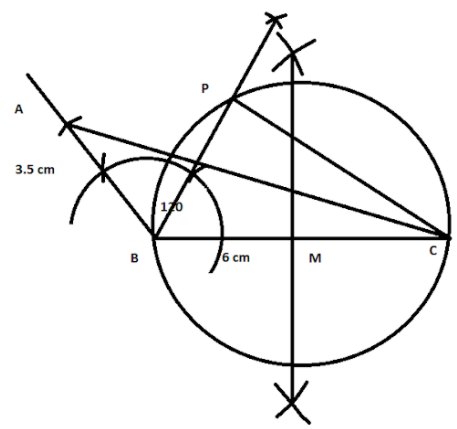
Joining C and P and measuring the angle we get,

Note: In this problem, we are to measure the angle we get in the last step. Sometimes, it might be the case that once we get the figure and we try to measure the angle, we will get the angles are not in whole numbers or in integers all the time. Then, we will try to consider it as a calculation problem and we will choose the nearest integer to get the solution.
Recently Updated Pages
Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
Who was appointed as the first chairman of the Indian class 10 social science CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

Five things I will do to build a great India class 10 english CBSE

Ladang is the name given to shifting cultivation in class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Write a letter to the principal requesting him to grant class 10 english CBSE




