Question

Using a protractor, draw an angle of measure \[72^\circ \]. With this angle as given, draw angles of measure \[36^\circ \] and \[54^\circ \].

Answer 1

Hint: Here, we will draw an angle ABC of \[72^\circ \] with the help of a protractor. Then with a center B and any radius, we will draw an arc, which intersect AB at D and BC at E and center D and E and radius more than \[\dfrac{{{\text{DE}}}}{2}\] and then draw two arcs which intersect each other at F. Then we will Join FB, which intersect the arc at G. So with centers D and G and radius more than \[\dfrac{{{\text{DE}}}}{2}\] and we will draw two arcs which intersect each other at F. Now with centers D and G and radius more than \[\dfrac{{{\text{DG}}}}{2}\] draw two arcs, which intersect each other at H and we will join HB to find the required angles.

Complete step-by-step answer:
First, we will draw an angle ABC of \[72^\circ \] with the help of a protractor.

Then with a center B and any radius, we will draw an arc, which intersects AB at D and BC at E.
With center D and E and radius more than \[\dfrac{{{\text{DE}}}}{2}\] and then draw two arcs which intersect each other at F.
Then we will Join FB, which intersects the arc at G.
So with centers D and G and radius more than \[\dfrac{{{\text{DE}}}}{2}\] and we will draw two arcs which intersect each other at F.
Now with centers D and G and radius more than \[\dfrac{{{\text{DG}}}}{2}\] draw two arcs which intersect each other at H.
Joining HB, we get

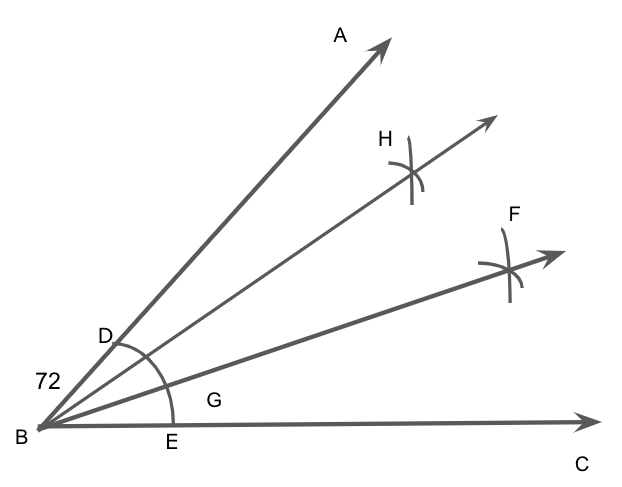
Therefore this implies that \[\angle HBC = 54^\circ \] and \[\angle FBC = 36^\circ \].

Note: The crucial part of this problem is to use the compass properly. One needs to know the basic rules and way of using a compass. We will verify our angle by using the protractor and putting it on the line BC with B as a center. This is a simple problem, we have to be careful with the labeling of the arcs as well.