Question

Using $ 30 - 60 - 90 $ degree triangle theorem, find the shortest and longest side of the given triangle.

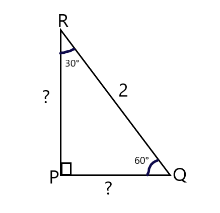
A.Shortest side $ = 1 $ , longest side $ = \sqrt 3 $
B.Shortest side $ = 2 $ , longest side $ = \sqrt 3 $
C.Shortest side $ = 1 $ , longest side $ = 2\sqrt 3 $
D.Shortest side $ = 1 $ , longest side $ = \sqrt 2 $

Answer 1

Hint: In order to find the longest and shortest side for the figure using the theorem of $30 - 60 - 90$ degree, we should know the properties related to this theorem, that is the length of the sides of this triangle is always constant that is $1:2:\sqrt 3 $ . Compare this value with the values given in the figure.

Complete step by step solution:
 $ 30 - 60 - 90 $ is a special triangle whose sides are always constant that is in the ratio $ 1:2:\sqrt 3 $ .
The figure given is:

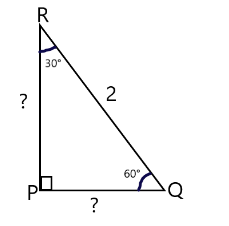
According to the figure, we are given that the hypotenuse (RQ) is of the length $ 2 $ unit.
From the angle and side theorem we know that the side opposite to the largest angle is the largest.
Since, the largest angle is of right angle that is $ {90^ \circ } $ , so the largest side is RQ, but leaving that we need to find the largest and shortest side.
So, leaving the $ {90^ \circ } $ , the largest angle is \[{60^ \circ }\], so the side opposite to this would be the longest that is side RP.
Similarly, the side opposite to the shortest angle that is $ {30^ \circ } $ would be the shortest and that is PQ.
From the $ 30 - 60 - 90 $ degree triangle theorem, we know that:
Shortest side is equal to half of the hypotenuse.
And, Longest side is equal to the shortest side multiplied by $ \sqrt 3 $ .
Using these properties, we get:
Shortest side (RP) $ = \dfrac{1}{2} \times $ hypotenuse $ = \dfrac{1}{2} \times 2 = 1 $ .
Longest side (PQ) $ = \sqrt 3 \times $ shortest side $ = \sqrt 3 \times 1 = \sqrt 3 $ .
Therefore, option A is correct, that is: Shortest side $ = 1 $ , longest side $ = \sqrt 3 $ .
So, the correct answer is “Option A”.

Note:
I.It’s important to use the properties if it is specifically mentioned in the question.
II.If instead the hypotenuse, the other side was given then also the properties would be the same.
III.If the angles are different then, these properties would not be followed.