Question

Using \[1AU\](mean earth-sun distance) = \[1.5 \times {10^{11}}m\] and parsec as distance at which \[1AU\] subtends an angle of one arcsecond, find parsec in meters.

Answer 1

Hint : One AU is defined to be the distance between the sun and earth. One AU subtending angle means drawing a line from earth to target. Another line drew from the sun and that same target that two lines met to create an angle. The angle happens to be one arc second so the distance from the sun to the target is defined as one parsec.

Complete step-by-step solution:
Astronomical Unit(AU):
The astronomical unit is the unit of length. The average distance of the earth from the sun. The metric of AU is\[1.495978707 \times {10^{11}}\;m\]. It is used to measure distances within the solar system or other stars. There are also other components in the definition of another unit in astronomical length, the parsec.
\[1AU = 1.5 \times {10^{11}}m\]
Parsec:
Distance to a star that subtends an angle of \[1\]arc second at an arc length\[1AU\]. A parsec is a unit of length, not a time. The parsec unit has an origin is one of the methods to determine distance to the stars.
A parsec unit is a distance to stars' apparent positions shifted by \[1\]arc second in the sky.

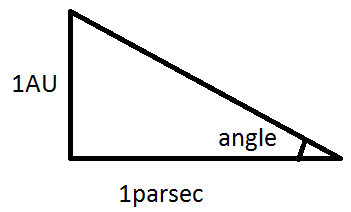
\[\tan \theta = \dfrac{{1AU}}{{1par\sec }}\]
We know,
\[{180^ \circ } = \pi {\text{ }}radian\]
And,
\[{1^{^ \circ }} = 3600\sec \]
\[ \Rightarrow {180^ \circ } = {180^ \circ } \times 3600\sec \]
\[ \Rightarrow 1\sec = \dfrac{{\pi \times 1}}{{180 \times 3600}}radian\]
\[ \Rightarrow \tan \theta = \dfrac{{1AU}}{{1par\sec }}\]
\[ \Rightarrow \tan \theta \approx \theta \]
\[ \Rightarrow \theta = \dfrac{{1AU}}{{1par\sec }}\]
\[ \Rightarrow 1par\sec = \dfrac{{1AU}}{\theta }\]
\[ \Rightarrow 11par\sec = \dfrac{{1.5 \times {{10}^{11}} \times 180 \times 3600}}{\pi }\]
\[ \Rightarrow 1par\sec = \dfrac{{1.5 \times {{10}^{11}} \times 180 \times 3600}}{{3.14}}m\]
\[\therefore 1par\sec = 3.09 \times {10^{16}}m\]
Hence, the parsec in meters is \[3.09 \times {10^{16}}m\].

Note:The Astronomical Unit of length effectively equal to the average distance between the earth and the sun. The Parsec unit is used to determine the distance to the stars. The unit of parsec is much bigger than\[AU\].