Question

How do you use the unit circle to find the exact value of \[\cos \left( \dfrac{7\pi }{3} \right)\]?

Answer 1

Hint: To solve these types of problems, we should know some of the trigonometric properties. The first one is, \[\cos (2\pi +x)=\cos x\]. This is true because when a point completes one rotation and comes back in the first quadrant its reference angle equals \[\theta -2\pi \], where \[\theta \] is the total angle rotated by the point.

Complete answer:

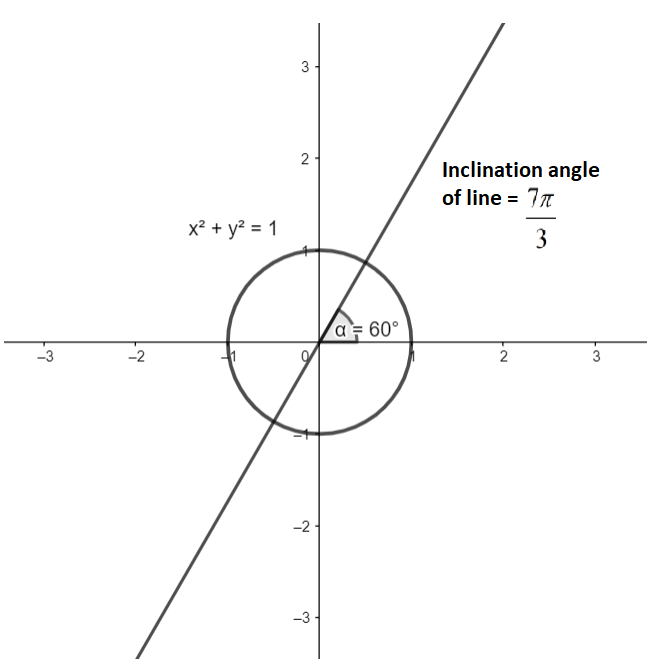
We are asked to find the value of the \[\cos \left( \dfrac{7\pi }{3} \right)\]. From the given figure we can see that the unit circle and the coordinate axes have divided the coordinate plane into 4 sectors. Each of those sectors is the quadrant of the coordinate axes.
As we can see that the line with the inclination \[\dfrac{7\pi }{3}\], lies in the first quadrant. As it has completed a full rotation before coming back in the first sector. The angle can be written in the form of \[2\pi +x\]. Comparing this with the inclination of the line, we get
\[\Rightarrow 2\pi +x=\dfrac{7\pi }{3}\]
Subtracting \[2\pi \] from both sides of the above equation, we get
\[\begin{align}
  & \Rightarrow 2\pi +x-2\pi =\dfrac{7\pi }{3}-2\pi \\
 & \Rightarrow x=\dfrac{\pi }{3} \\
\end{align}\]
we want to find the value of \[\cos \left( \dfrac{7\pi }{3} \right)\]. As we have seen the angle \[\dfrac{7\pi }{3}\] can also be written as \[2\pi +\dfrac{\pi }{3}\]. Using this in the evaluation of the value of the \[\cos \left( \dfrac{7\pi }{3} \right)\], we get
\[\Rightarrow \cos \left( \dfrac{7\pi }{3} \right)=\cos \left( 2\pi +\dfrac{\pi }{3} \right)\]
We know the property \[\cos (2\pi +x)=\cos x\], using this in the for the above expression we get
\[\Rightarrow \cos \left( 2\pi +\dfrac{\pi }{3} \right)=\cos \left( \dfrac{\pi }{3} \right)\]
As we know that the value of \[\cos \left( \dfrac{\pi }{3} \right)\] is \[\dfrac{1}{2}\].
Hence, the value of \[\cos \left( \dfrac{7\pi }{3} \right)\] equals \[\dfrac{1}{2}\].

Note: The line drawn in the figure is just for reference, it is to show the angle of inclination \[\dfrac{7\pi }{3}\]. The question can be solved without it. Also, to solve these types of problems, one should know the trigonometric properties of the ratios.