Question

Use the unit circle to derive \[\sin \left( {2\pi - \theta } \right)\].

Answer 1

Hint: An unit circle is a circle of radius \[1\] unit whose various arc lengths determine the values of trigonometric functions.

Complete step by step solution:
A unit circle is a circle of radius \[1\] unit. For every real number \[x\] represented by a point \[P\] on the real axis, there exists a point \[P'\] on the unit circle with the center at the origin of the coordinate system such that the radian measure of \[\angle AOP\] is \[x\] so the arc length \[AP\] \[ = \] \[x\].

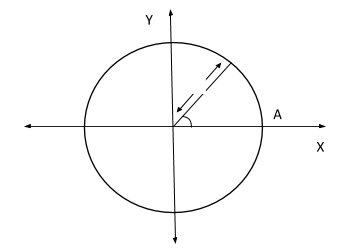
Then on the unit circle we define cosine and sine functions of radian measure (for any real number \[x\]) as:
\[\cos x = a\], \[\sin x = b\]
Now you have to find the value of \[\sin \left( {2\pi - \theta } \right)\]:
Using the formula:
 \[\sin \left( {a - b} \right)\] \[ = \] \[\sin a\cos b - \cos a\sin b\]
Find \[\sin (2\pi - \theta )\]:
\[\sin (2\pi - \theta )\] \[ = \] \[\sin 2\pi \cos \theta - \cos 2\pi \sin \theta \]
\[ \Rightarrow \] \[\sin (2\pi - \theta )\] \[ = \] \[0 - \sin \theta \]
\[ \Rightarrow \] \[\sin (2\pi - \theta )\] \[ = \] \[ - \sin \theta \]
In the first step it is already shown how to find the value of \[\sin \theta \] for any real \[\theta \] from the unit circle then the negative of that will be equal to the value of \[\sin \left( {2\pi - \theta } \right)\].

Note: Students must remember the following conversions:
\[\sin \left( {2\pi - \theta } \right)\] \[ = \] \[ - \sin \theta \]
\[\sin \left( {2\pi + \theta } \right)\] \[ = \] \[\sin \theta \]
 \[\sin \left( {\pi - \theta } \right)\] \[ = \] \[\sin \theta \]
 \[\sin \left( {\pi + \theta } \right)\] \[ = \] \[ - \sin \theta \]
The same conversations must also be remembered for other trigonometric functions. The derivations as shown in the solution must be done for understanding but memorising the conversions are useful for quick application.