
Use the table given below to draw the graph,
x -5 -1 3 b 13 y -2 a 2 5 7
From your graphs, find the values of “a” and “b”. State a linear relation between the variables x and y.
| x | -5 | -1 | 3 | b | 13 |
| y | -2 | a | 2 | 5 | 7 |
Answer
573k+ views
Hint: We have given a table of x and y coordinates of the 5 points and we are asked to draw its graph and find the values of “a” and “b”. Now, to draw the given points on the graph paper take the three points in which no coordinate contains “a” or “b” and locate those points on the graph paper then draw a line passing through these three points. After getting a line, to find the values of “a” and “b”, see when x equals -1 on the straight line then what is the corresponding value of y (which is “a”) and to find the value of b see when y equals 5 on the straight line then what is the corresponding x. After that we are also asked to find the linear relation between x and y so assume the linear relation as $y=mx+c$ and substitute any two points given in the above table in this linear relation and hence, get the value of m and c.
Complete step by step answer:
In the above question, we have given a table of 5 points having x and y coordinates as follows:
We are asked to locate these points on the graph and then find the values of “a” and “b”.
So, we are going to locate the above 3 points of the above table which do not contain any “a” or “b” on the graph paper and join the three points and see which curve we are getting.
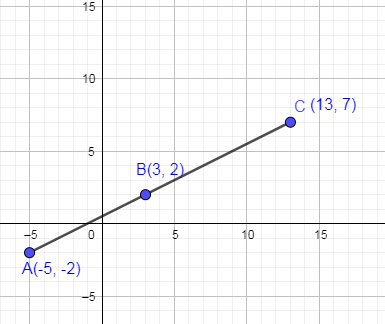
As you can see from the above figure that after locating the three points which did not contain “a” and “b we are getting a straight line.
Now, we are going to find the value of “a” and “b” as follows:
To find the value of “a” we have to see when x equals -1 on the straight line that we have drawn then what is the value of corresponding y coordinate.
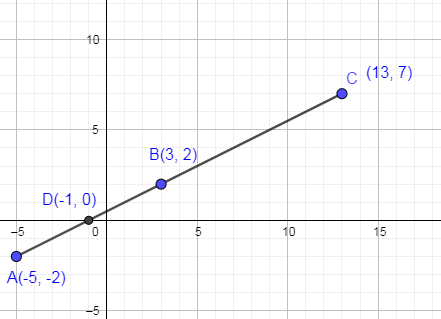
From the above graph, you can see that the y coordinate corresponding to x equals -1 is 0. Hence, the value of “a” is equal to 0.
To find the value of b, we have to see on which value of x, the y coordinate on the straight line is 5 which we are shown below by using the graph:
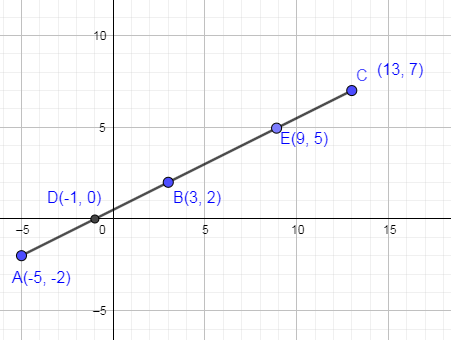
From the above graph, you can see that when y on the straight line is 5 then x corresponding to that y is 9. Hence, the value of “b” is equal to 9.
Now, we have to write a linear relation between x and y. We know that the linear relation between x and y is written as:
$y=mx+c$ ……….Eq. (1)
Substituting any two points given in the table to find the values of unknowns m and c in the above equation.
Substituting the point (-5, -2) and (3, 2) in the above linear equation we get,
$\begin{align}
& -2=m\left( -5 \right)+c......Eq.(2) \\
& 2=m\left( 3 \right)+c.........Eq.(3) \\
\end{align}$
Subtracting eq. (2) from eq. (3) we get,
$\begin{align}
& 2-\left( -2 \right)=3m-\left( -5m \right)+0 \\
& \Rightarrow 2+2=3m+5m \\
& \Rightarrow 4=8m \\
& \Rightarrow m=\dfrac{4}{8} \\
& \Rightarrow m=\dfrac{1}{2} \\
\end{align}$
Now, substituting the above value of m in eq. (2) we get,
$\begin{align}
& -2=\dfrac{1}{2}\left( -5 \right)+c \\
& \Rightarrow -2+\dfrac{5}{2}=c \\
& \Rightarrow \dfrac{-4+5}{2}=c \\
& \Rightarrow \dfrac{1}{2}=c \\
\end{align}$
Now, substituting the above calculated values of m and c in eq. (1) we get,
$\begin{align}
& y=\dfrac{1}{2}x+\dfrac{1}{2} \\
& y=\dfrac{x+1}{2} \\
& \Rightarrow 2y=x+1 \\
\end{align}$
Hence, we have got the relation between the variables x and y as $2y=x+1$.
Note: In the above problem, the alternative way to find the values of “a” and “b” is to use the linear relation that we have solved above.
The linear relation that we solved above is:
$2y=x+1$
Now, to find the value of “a”, substituting the value of x as -1 in the above equation then the value of y that we will get is the value of “a”.
$\begin{align}
& 2y=-1+1 \\
& \Rightarrow 2y=0 \\
& \Rightarrow y=0 \\
\end{align}$
Hence, we got the value of “a” as 0.
To get the value of “b”, substituting the value of y as 5 in the above linear equation then the value of x is the value of “b”.
$\begin{align}
& 2\left( 5 \right)=x+1 \\
& \Rightarrow 10-1=x \\
& \Rightarrow 9=x \\
\end{align}$
Hence, we got the value of “b” as 9.
We can see from the values of “a” and “b” that the alternative method is giving is the same as that we have solved above. So, this method also verifies the values of “a” and “b” that we are getting above.
Complete step by step answer:
In the above question, we have given a table of 5 points having x and y coordinates as follows:
| x | -5 | -1 | 3 | b | 13 |
| y | -2 | a | 2 | 5 | 7 |
We are asked to locate these points on the graph and then find the values of “a” and “b”.
So, we are going to locate the above 3 points of the above table which do not contain any “a” or “b” on the graph paper and join the three points and see which curve we are getting.

As you can see from the above figure that after locating the three points which did not contain “a” and “b we are getting a straight line.
Now, we are going to find the value of “a” and “b” as follows:
To find the value of “a” we have to see when x equals -1 on the straight line that we have drawn then what is the value of corresponding y coordinate.

From the above graph, you can see that the y coordinate corresponding to x equals -1 is 0. Hence, the value of “a” is equal to 0.
To find the value of b, we have to see on which value of x, the y coordinate on the straight line is 5 which we are shown below by using the graph:

From the above graph, you can see that when y on the straight line is 5 then x corresponding to that y is 9. Hence, the value of “b” is equal to 9.
Now, we have to write a linear relation between x and y. We know that the linear relation between x and y is written as:
$y=mx+c$ ……….Eq. (1)
Substituting any two points given in the table to find the values of unknowns m and c in the above equation.
Substituting the point (-5, -2) and (3, 2) in the above linear equation we get,
$\begin{align}
& -2=m\left( -5 \right)+c......Eq.(2) \\
& 2=m\left( 3 \right)+c.........Eq.(3) \\
\end{align}$
Subtracting eq. (2) from eq. (3) we get,
$\begin{align}
& 2-\left( -2 \right)=3m-\left( -5m \right)+0 \\
& \Rightarrow 2+2=3m+5m \\
& \Rightarrow 4=8m \\
& \Rightarrow m=\dfrac{4}{8} \\
& \Rightarrow m=\dfrac{1}{2} \\
\end{align}$
Now, substituting the above value of m in eq. (2) we get,
$\begin{align}
& -2=\dfrac{1}{2}\left( -5 \right)+c \\
& \Rightarrow -2+\dfrac{5}{2}=c \\
& \Rightarrow \dfrac{-4+5}{2}=c \\
& \Rightarrow \dfrac{1}{2}=c \\
\end{align}$
Now, substituting the above calculated values of m and c in eq. (1) we get,
$\begin{align}
& y=\dfrac{1}{2}x+\dfrac{1}{2} \\
& y=\dfrac{x+1}{2} \\
& \Rightarrow 2y=x+1 \\
\end{align}$
Hence, we have got the relation between the variables x and y as $2y=x+1$.
Note: In the above problem, the alternative way to find the values of “a” and “b” is to use the linear relation that we have solved above.
The linear relation that we solved above is:
$2y=x+1$
Now, to find the value of “a”, substituting the value of x as -1 in the above equation then the value of y that we will get is the value of “a”.
$\begin{align}
& 2y=-1+1 \\
& \Rightarrow 2y=0 \\
& \Rightarrow y=0 \\
\end{align}$
Hence, we got the value of “a” as 0.
To get the value of “b”, substituting the value of y as 5 in the above linear equation then the value of x is the value of “b”.
$\begin{align}
& 2\left( 5 \right)=x+1 \\
& \Rightarrow 10-1=x \\
& \Rightarrow 9=x \\
\end{align}$
Hence, we got the value of “b” as 9.
We can see from the values of “a” and “b” that the alternative method is giving is the same as that we have solved above. So, this method also verifies the values of “a” and “b” that we are getting above.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Why is there a time difference of about 5 hours between class 10 social science CBSE

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Which is the largest Gulf in the world A Gulf of Aqaba class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it




