Question

How do you use the Pythagorean Theorem to solve for the missing side given a = 7, c = 21?

Answer 1

Hint: In this problem we have to use the Pythagorean Theorem to find the missing side of the right triangle with the given measures where we can assume c as the hypotenuse and we have a = 7, c = 21. We know that the Pythagoras Theorem is \[{{a}^{2}}+{{b}^{2}}={{c}^{2}}\]. We can see that, we are already given the value for a and c, which we can substitute in the formula where the missing side is b, which we have to find.

Complete step by step solution:
We know that we have used the Pythagorean Theorem to find the missing side of the right triangle with the given measures given c is the hypotenuse and we have a = 7, c = 21.

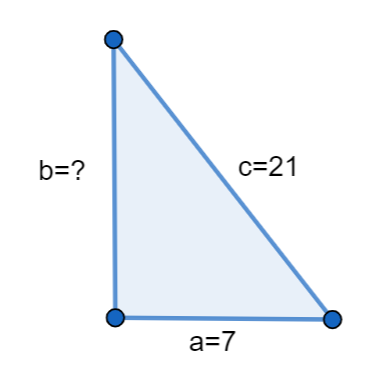
We know that the Pythagoras Theorem is \[{{a}^{2}}+{{b}^{2}}={{c}^{2}}\].
We can substitute the value a = 7, c = 21 in the above formula, we get
\[\Rightarrow {{7}^{2}}+{{b}^{2}}={{21}^{2}}\]
We can now simplify the above step, we get
\[\begin{align}
  & \Rightarrow {{b}^{2}}=441-49 \\
 & \Rightarrow {{b}^{2}}=392 \\
\end{align}\]
We can now take square root on both sides, we get
\[\Rightarrow b=\sqrt{392}=19.79\]
Therefore, the missing side of the given right triangle is \[\sqrt{392}\]units.

Note: Students should remember the Pythagoras theorem formula is \[{{a}^{2}}+{{b}^{2}}={{c}^{2}}\]. Where the sum of squares of two sides is equal to the square of the hypotenuse. We should also see that the given triangle should be a right-angle triangle, where Pythagora's theorem is only applied to right-angled triangles.