Question

Use the following images to answer the questions. (a) How are the triangles similar? Justify your answer with a theorem or postulate. (b) What is the value of x?

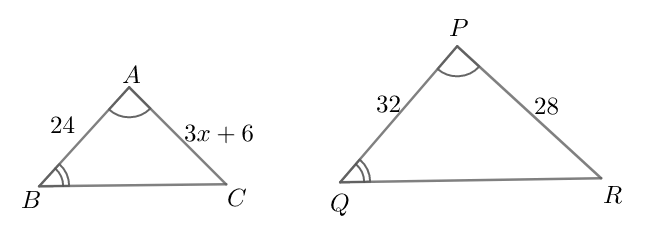
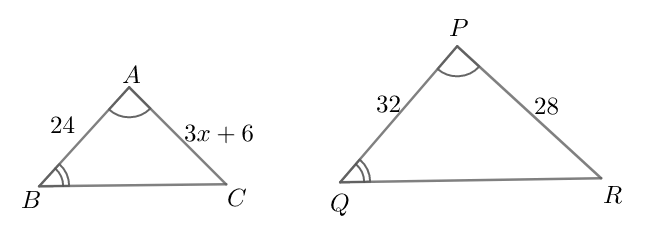
Answer 1

Hint: In the two figures, we can see that the two corresponding angles are equal. This means the two triangles are similar according to the AA axiom of similarity. After that, we use the “corresponding parts of similar triangles are proportionate” theorem to find the value of x.

Complete step by step answer:
In Euclidean geometry, two objects are said to be similar if they have the same shape. They may or may not have the same size. Similarly, two objects are said to be congruent if they have the same shape and size. Thus, we can understand that only shape is the determining factor if two objects are similar or not and both shape and size are the determining factors for two objects to be congruent.
There are various axioms, theorems or postulates that define similarity of two objects. For triangles, one of these axioms is angle-angle-angle which is abbreviated as AAA axiom of similarity of triangles. This axiom states that if all the three corresponding angles of two triangles are same then, the two triangles are similar. But, the proof of only two of the angles is sufficient as the third angle is always bound by the sum of angles of a triangle property.
In $\Delta ABC$ and $\Delta PQR$ ,

$\angle B=\angle Q$	given
$\angle A=\angle P$	given
$\Delta ABC\tilde{\ }\Delta PQR$	AA axiom of similarity

We know that if two triangles are similar, then the corresponding sides are in proportion. This means,
\[\begin{align}
  & \Rightarrow \dfrac{AB}{PQ}=\dfrac{AC}{PR} \\
 & \Rightarrow \dfrac{24}{32}=\dfrac{3x+6}{28} \\
 & \Rightarrow 3x+6=\dfrac{24}{32}\times 28 \\
 & \Rightarrow x=5 \\
\end{align}\]
Therefore, we can conclude that the two triangles are similar and the value of x is $5$

Note: In the proofs of similarity, we must carefully observe the figures and then decide else, we either cannot find a clue or end up with wrong answers. Most of the students commit mistakes in the proportionality part where we find the unknown side by proportionality. We must do it carefully.