Question

How‌ ‌do‌ ‌you‌ ‌use‌ ‌the‌ ‌first‌ ‌and‌ ‌second‌ ‌derivatives‌ ‌to‌ ‌sketch‌ ‌$y=\dfrac{{{e}^{x}}}{x}?$‌ ‌ ‌

Answer 1

Hint: To solve this question, we need to use the first and second derivatives for the given equation and use the information from this to plot the given function. First, we try to find the roots of the given equation. Next, we use the first derivative to find the critical points. We then use the second derivative to find whether there exists a maxima or minima at these critical points. Using these, we can plot the graph.

Complete step-by-step solution:
Let us first calculate the roots of this equation $y=\dfrac{{{e}^{x}}}{x}.$ To do so, we equate y=0 and solve the equation.
$\Rightarrow 0=\dfrac{{{e}^{x}}}{x}$
Cross multiplying x with 0, we get
$\Rightarrow {{e}^{x}}=0$
Since ${{e}^{x}}$ is always greater than x for any value of x, there exists no roots for this given equation.
Next, we need to calculate the first derivative of the first derivative in order to find the critical points. We use the quotient rule of differentiation for this. This is given by,
$\Rightarrow \dfrac{d}{dx}\left( \dfrac{u}{v} \right)=\dfrac{v\dfrac{du}{dx}-u\dfrac{dv}{dx}}{{{v}^{2}}}$
From the given equation, we know that $u={{e}^{x}}$ and $v=x.$ Substituting these in the formula,
$\Rightarrow \dfrac{dy}{dx}=\dfrac{x\dfrac{d\left( {{e}^{x}} \right)}{dx}-{{e}^{x}}\dfrac{d\left( x \right)}{dx}}{{{x}^{2}}}$
We know that the differentiation of ${{e}^{x}}$ with respect to x is ${{e}^{x}}$ itself and differentiation of x with respect to x is 1.
$\Rightarrow \dfrac{dy}{dx}=\dfrac{x{{e}^{x}}-{{e}^{x}}}{{{x}^{2}}}$
Taking the ${{e}^{x}}$ common in the numerator,
$\Rightarrow \dfrac{dy}{dx}=\dfrac{{{e}^{x}}\left( x-1 \right)}{{{x}^{2}}}$
To find the critical point, we need to equate this derivate to 0.
$\Rightarrow \dfrac{dy}{dx}=0$
$\Rightarrow \dfrac{{{e}^{x}}\left( x-1 \right)}{{{x}^{2}}}=0$
Cross multiplying ${{x}^{2}},$
$\Rightarrow {{e}^{x}}\left( x-1 \right)=0$
This means that,
$\Rightarrow {{e}^{x}}=0$ and $\Rightarrow \left( x-1 \right)=0$
We know that there is no solution for the first equation and solving for the second equation by taking the -1 to the other side,
$\Rightarrow x=1$
Substituting this in $y=\dfrac{{{e}^{x}}}{x},$
$\Rightarrow y=\dfrac{{{e}^{1}}}{1}=e$
Hence there exists a critical point at $\left( 1,e \right).$
Now we use the second derivative to find the maxima or minima. Using the quotient rule again for the first derivative $\dfrac{dy}{dx}=\dfrac{x{{e}^{x}}-{{e}^{x}}}{{{x}^{2}}},$
Splitting the terms and cancelling the x term in the first term, we can rewrite this as,
$\Rightarrow \dfrac{dy}{dx}=\dfrac{{{e}^{x}}}{x}-\dfrac{{{e}^{x}}}{{{x}^{2}}}$
We now differentiate this equation now. We already know the derivative for the first term so we substitute that directly. For the second term, we apply the quotient rule
$\Rightarrow \dfrac{{{d}^{2}}y}{d{{x}^{2}}}=\dfrac{\left( x-1 \right){{e}^{x}}}{{{x}^{2}}}-\dfrac{d}{dx}\left( \dfrac{{{e}^{x}}}{{{x}^{2}}} \right)$
Differentiating the second term using the quotient rule,
$\Rightarrow \dfrac{{{d}^{2}}y}{d{{x}^{2}}}=\dfrac{\left( x-1 \right){{e}^{x}}}{{{x}^{2}}}-\dfrac{{{x}^{2}}\dfrac{d\left( {{e}^{x}} \right)}{dx}-{{e}^{x}}\dfrac{d\left( {{x}^{2}} \right)}{dx}}{{{x}^{4}}}$
We know that the differentiation of ${{e}^{x}}$ with respect to x is ${{e}^{x}}$ itself and differentiation of ${{x}^{2}}$ with respect to x is 2x.
$\Rightarrow \dfrac{{{d}^{2}}y}{d{{x}^{2}}}=\dfrac{\left( x-1 \right){{e}^{x}}}{{{x}^{2}}}-\dfrac{{{x}^{2}}{{e}^{x}}-2x{{e}^{x}}}{{{x}^{4}}}$
To find out of it is a maxima or minima, we substitute the critical point, that is x=1.
$\Rightarrow \dfrac{{{d}^{2}}y}{d{{x}^{2}}}=\dfrac{\left( 1-1 \right){{e}^{1}}}{{{1}^{2}}}-\dfrac{{{1}^{2}}{{e}^{1}}-2.1.{{e}^{1}}}{{{1}^{4}}}$
First term is 0 and second term had e and 2e subtracted,
$\Rightarrow \dfrac{{{d}^{2}}y}{d{{x}^{2}}}=-\left( e-2e \right)=e$
This second derivative is positive indicating a minima at x=1.
Using all the information, we can plot the curve for $y=\dfrac{{{e}^{x}}}{x}.$

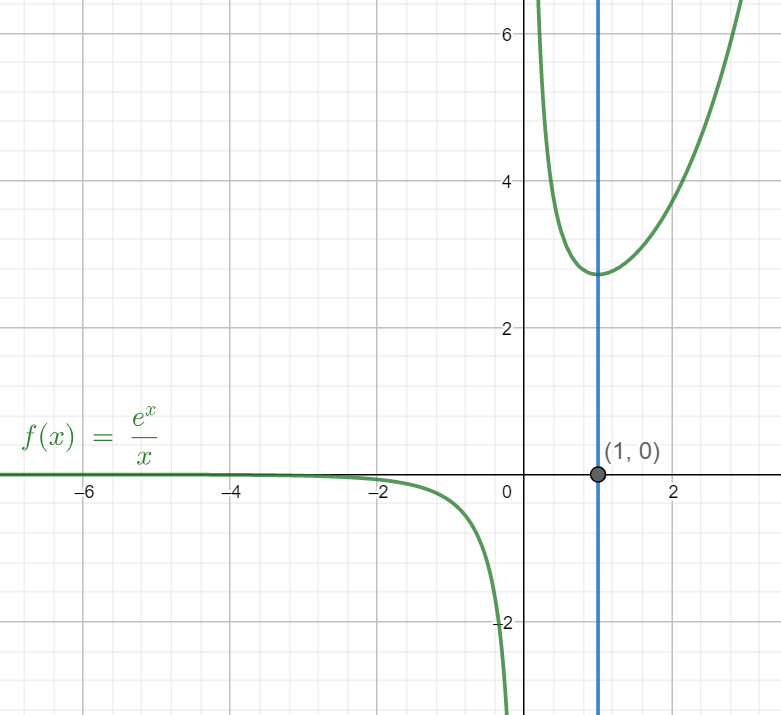
We can see that there are no roots meaning there is no intersection with the y-axis. We also see a minima for the curve at x=1.
Hence, we have used the first and second derivatives to sketch $y=\dfrac{{{e}^{x}}}{x}.$

Note: To solve this question, the students need to know the quotient rule of differentiation very well. They must have a thorough understanding of the topic of differentiation in order to solve such sums easily. They should also know the method of finding a minima and maxima using the first and second derivatives.