Question

Use the figure alongside to find the value of $y$ in terms of $x$. Calculate $y$, if $x = 5^\circ $

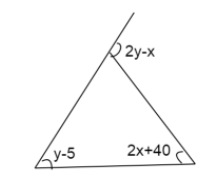
A) $y = 3x + 35{\text{ and }}y = 20^\circ $
B) $y = 3x + 35{\text{ and }}y = 50^\circ $
C) $y = 3x + 35{\text{ and }}y = 40^\circ $
D) $y = 3x + 35{\text{ and }}y = 90^\circ $

Answer 1

Hint: The angles of the triangle are denoted using the variables $x$ and $y$. The value of $x$ is given. We can find the value of $y$ using the results of angle in a line and sum of angles in a triangle.

Formula used:
The angle in a line is $180^\circ $.
The sum of angles in a triangle is $180^\circ $.

Complete step-by-step answer:

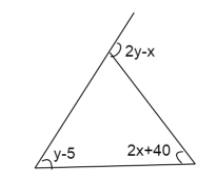
In the given triangle, let name the points A, B, C and P.
We know that angle in a line is $180^\circ $.
We can see that in the vertex A, $\angle PAC$ and $\angle CAB$ are supplementary.
So we have, $\angle PAC + \angle CAB = 180^\circ - - - (i)$
It is given that $\angle PAC = 2y - x$.
Also it is given that, $x = 5^\circ $.
So we get, $\angle PAC = 2y - 5^\circ $
Substituting for $\angle PAC$ in equation $(i)$ we have,
$2y - 5^\circ + \angle CAB = 180^\circ $
This gives, $\angle CAB = 180^\circ - 2y + 5^\circ = 185^\circ - 2y$
Now consider, $\vartriangle ABC$.
We know that the sum of angles in a triangle is $180^\circ $.
That is, $\angle A + \angle B + \angle C = 180^\circ - - - (ii)$.
We have, $\angle A = \angle CAB = 185^\circ - 2y$
$\angle B = y - 5^\circ $
$\angle C = 2x + 40^\circ = 2 \times 5^\circ + 40^\circ = 50^\circ $
Substituting these in equation $(ii)$ we have,
$185^\circ - 2y + y - 5^\circ + 50^\circ = 180^\circ $
Simplifying we get,
$230^\circ - y = 180^\circ $
$ \Rightarrow y = 230^\circ - 180^\circ = 50^\circ $
We have $50 = 15 + 35$.
Also since $x = 5^\circ $, $y = 3x + 35^\circ $
$\therefore $ The answer is option B.

Note: We can approach the question in another way.
While considering the triangle ABC, we can see $\angle PAC$ as an external angle. We know that the sum of two internal angles of a triangle is equal to the external angle at the third vertex.
So we have, $\angle B + \angle C = \angle PAC$
Substituting the values we get,
$y - 5 + 2x + 40 = 2y - x$
Simplifying we get,
$x + 35 = y$
Thus we get the relation between $x$ and $y$.
Now substituting the value of $x$, we get the value of $y$.