Question

How do you use synthetic division to divide \[\dfrac{{{x^5} - 13{x^4} - 120x + 80}}{{x + 3}}\]?

Answer 1

Hint:
In the given question, we have been asked to calculate the value of a given polynomial expression. The given expression is a fraction with the numerator consisting of a polynomial of degree five, while the denominator of the expression is a polynomial of degree one. We have to divide the two things. To solve this though, we have to use synthetic division. To do that, we need to make sure of just two things – the term in the denominator is of degree one and that its coefficient is one, which in our question is being satisfied.

Complete step by step solution:
We have to solve for the given expression, which is – \[\dfrac{{{x^5} - 13{x^4} - 120x + 80}}{{x + 3}}\].
For solving this, we are going to add the square and cube terms in the numerator, so that it becomes a full polynomial of the given degree, so it becomes,
\[\dfrac{{{x^5} - 13{x^4} + 0{x^3} + 0{x^2} - 120x + 80}}{{x + 3}}\]
Now, we write just the coefficients of the numerators and the negative of the constant term in the denominator inside the box. Then we are going to multiply the first coefficient with the negative of the constant term, subtract them, then multiply the difference and the negative of the constant term, and keep on repeating till we reach the last term (which is the constant term of the numerator). Then, the subtracted numbers are going to give us the coefficients of the quotient. And that is going to be our answer

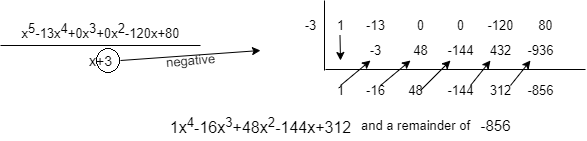
Hence, on division, we get the quotient \[{x^4} - 16{x^3} + 48{x^2} - 144x + 312\] with a remainder of \[ - 856\].

Thus, \[\dfrac{{{x^5} - 13{x^4} - 120x + 80}}{{x + 3}} = {x^4} - 16{x^3} + 48{x^2} - 144x + 312 + \dfrac{{\left( { - 856} \right)}}{{x + 3}}\].

Additional Information:
This method of synthetic term is very easy compared to the usual long division method, as it takes much less time to be solved and the amount of space occupied is quite less too. Plus, we do not need to think of the divisor at each step while subtracting from the dividend. We just need to remember the steps which are used in the method of synthetic division.

Note:
In the given question, we had to divide two polynomials using the method of synthetic division. To solve it, we only need to remember the steps of the synthetic division. It is important to note that this method for synthetic division can only be followed if the two conditions are met, i.e., the denominator is linear (has just one variable term of degree one), and the coefficient of the variable term is one.