Question

How do you use special right triangles to find the missing side lengths?

Answer 1

Hint: The given question, we have been asked to use a special triangle to find the missing side length. In order to proceed with the following question we need to talk about special triangles. Triangle is a 2D figure which has 3 sides, 3 angles and 3 vertices. There are two types of special triangles, Right angled triangle with angles $ {30^ \circ },{60^ \circ },{90^ \circ } $ and isosceles right angled triangle with angles $ {45^ \circ },{45^ \circ },{90^ \circ } $ . Right angled triangle is a triangle which has one angle to be $ {90^ \circ } $ . Isosceles right angled triangle is a triangle which has two sides and two angles the same, and one angle is $ {90^ \circ } $ .

Complete step by step solution:
We are given,
Two special triangles include-
 $ {45^ \circ },{45^ \circ },{90^ \circ } $
 $ {30^ \circ },{60^ \circ },{90^ \circ } $
Let’s see the triangle with angles $ {45^ \circ },{45^ \circ },{90^ \circ } $ .

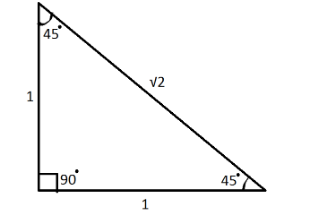
This is an isosceles right angled triangle. In this triangle $ perpendicular = base $ . We’ll assume $ perpendicular = base = 1 $ .We can use Pythagoras theorem to find the hypotenuse.
 $ {h^2} = {p^2} + {b^2} $
 $ \Rightarrow {h^2} = {1^2} + {1^2} $
 $ \Rightarrow {h^2} = 1 + 1 $
 $ \Rightarrow {h^2} = 2 $
 $ \Rightarrow h = \sqrt 2 $
The $ {45^ \circ },{45^ \circ },{90^ \circ } $ theorem states that triangles with these angles will have sides in ratio $ 1:1:\sqrt 2 $ , where side opposite to $ {45^ \circ } $ equate to $ 1 $ in the ratio and side opposite to $ {90^ \circ } $ equate to $ \sqrt 2 $ . To find the missing side, just put the given value in the following ratio and find the value. For example, side opposite to $ {45^ \circ } $ is given to be $ 5 $ . We can find missing values by comparing it with the ratio.
 $ \Rightarrow 1:1:\sqrt 2 $
Multiplying the equation by $ 5 $
 $ \Rightarrow (5)1:(5)1:(5)\sqrt 2 $
 $ \Rightarrow 5:5:5\sqrt 2 $
The missing side is $ 5\sqrt 2 $ .
Let’s see the triangle with angles $ {30^ \circ },{60^ \circ },{90^ \circ } $

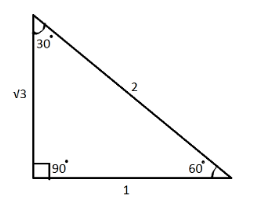
In the similar way, $ {30^ \circ },{60^ \circ },{90^ \circ } $ theorem states that triangles with these angles will have sides in ratio $ 1:\sqrt 3 :2 $ , where side opposite to $ {30^ \circ } $ equate to $ 1 $ in the ratio, side opposite to $ {60^ \circ } $ equates to $ \sqrt 3 $ and side opposite to $ {90^ \circ } $ equate to $ 2 $ . To find the missing side, just put the given value in the following ratio and find the value. For example, side opposite to $ {30^ \circ } $ is given to be $ 5 $ . We can find missing values by comparing it with the ratio.
 $ \Rightarrow 1:\sqrt 3 :2 $
Multiplying the equation by $ 5 $
 $ \Rightarrow (5)1:(5)\sqrt 3 :(5)2 $
 $ \Rightarrow 5:5\sqrt 3 :10 $
The missing sides are $ 5\sqrt 3 \;and\;10 $

Note: The Pythagorean Theorem needs two-side lengths; therefore, we can’t always rely on it to solve a right triangle for missing sides. When we have only one side, we can use a special triangle to find the remaining two terms. The side opposite to $ {90^ \circ } $ in a triangle is always known as hypotenuse.