Question

How do you use Pascal’s triangle to expand${(2x - y)^3}$?

Answer 1

Hint: Pascal’s triangle is an infinite equilateral triangle which consists of a sequence of numbers. It starts with 1. That means the first row is one. Then, the second row consist of the sum of two numbers above it. Similarly, we will find out the values of next rows. This creates a pattern of numbers as shown below.

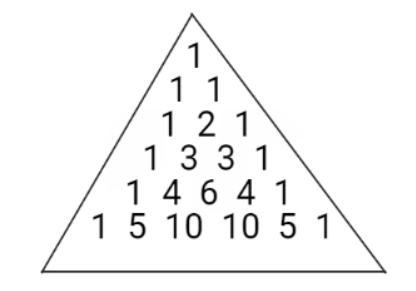
The main application of this triangle is to solve a binomial function. The triangle represents the coefficients of the binomial expansion. If the binomial equation is ${\left( {a + b} \right)^n}$. Then the expansion is ${C_1}{a^n}{b^0} + {C_2}{a^{n - 1}}{b^1} + ..... + {C_n}{a^0}{b^n}$, where ${C_1},{C_2},....,{C_n}$are the coefficients derived from the triangle .

Complete step by step answer:
We first derive the coefficients from the triangle where $n = 3$, which is depicted below:

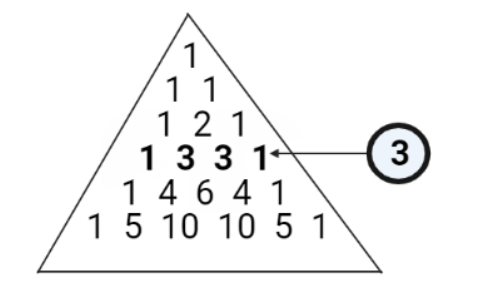
Hence we get, ${(a + b)^3} = 1{a^3}{b^0} + 3{a^2}{b^1} + 3{a^1}{b^2} + 1{a^0}{b^3}$
After substituting the value we get,
$
  {(2x - 3y)^3} = 1{(2x)^3}{( - 3y)^0} + 3{(2x)^2}{( - 3y)^1} + 3{(2x)^1}{( - 3y)^2} + 1{(2x)^0}{( - 3y)^3} \\
  {(2x - 3y)^3} = 8{x^3}.1 + 3(4{x^2})( - 3y) + 3(2x)(9{y^2}) + 1.1( - 27{y^3}) \\
  {(2x - 3y)^3} = 8{x^3} - 36{x^2}y + 54x{y^2} - 27{y^3} \\
 $
Hence, the expansion of ${(2x - y)^3}$ is $8{x^3} - 36{x^2}y + 54x{y^2} - 27{y^3}$.

Note: The Pascal’s triangle is helpful only when the value of $n$is small in the equation ${\left( {a + b} \right)^n}$. If the value of $n$is large , then it's tedious to draw the triangle until we reach n. Then, we should use combinations to expand the binomial expression.