
How do you use Pascal’s triangle to calculate the binomial coefficient of $\left( {\begin{array}{*{20}{c}} 9 \\ 4 \end{array}} \right)$ ?
Answer
471.3k+ views
Hint: Here we are asked to find the binomial coefficient of $\left( {\begin{array}{*{20}{c}} 9 \\ 4 \end{array}} \right)$ by using Pascal’s triangle. To solve this question, we first need to know about Pascal’s triangle. Pascal’s triangle is nothing but the numbers arranged in the triangular form which gives the coefficient in the expansion of binomial expressions, such as ${\left( {x + y} \right)^n}$ so, substituting the given terms in this form then find the position of the coefficient. With this position, we will find the coefficient from Pascal’s triangle.
Complete step by step answer:
It is given that $\left( {\begin{array}{*{20}{c}} 9 \\ 4 \end{array}} \right)$
Here $n = 9$ and $r = 4$. We aim to find the coefficient of this using Pascal’s triangle.
Let us first find the position of the coefficient by using the general form of any term in the form ${\left( {x + y} \right)^n}$. Any term of the form ${\left( {x + y} \right)^n}$ then it can be written as, ${\left( {x + y} \right)^n} = {x^{n - r}}{y^r}$.
Here for the given problem, $n = 9$ and $r = 4$ substituting this we get
${\left( {x + y} \right)^9} = {x^{9 - 4}}{y^4}$
${\left( {x + y} \right)^9} = {x^5}{y^4}$
Thus, we obtained the position of the coefficient.
Now let us draw Pascal’s triangle.
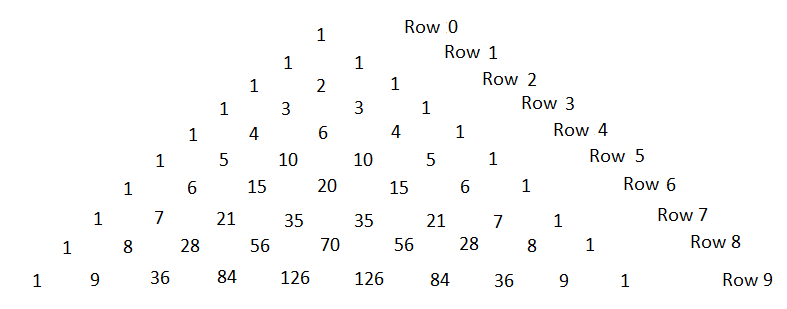
The ninth row of Pascal’s triangle gives us all the coefficients of all the terms in ${\left( {x + y} \right)^9}$ but we need to know the coefficient of the term having the variable ${x^5}{y^4}$. Let us get it from the ninth row of Pascal’s triangle.
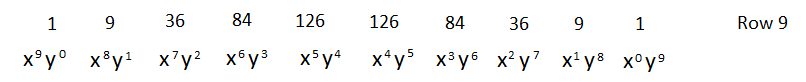
Thus, as we can see the above picture it is clear that the coefficient of the ${x^5}{y^4}$ is $126$ .
Hence, the coefficient of $\left( {\begin{array}{*{20}{c}} 9 \\ 4 \end{array}} \right)$ is $126$.
Note:
In the above problem, one must know how to draw Pascal’s triangle. It starts with the number $1$ that number branches out as two $1's$ after that for the next row we must add these two $1's$ and put it in the next row the sides are filled with ones always this step is repeated until we reach our required row. Here we stopped at the ninth row since the value of $n$ is $9$.
Complete step by step answer:
It is given that $\left( {\begin{array}{*{20}{c}} 9 \\ 4 \end{array}} \right)$
Here $n = 9$ and $r = 4$. We aim to find the coefficient of this using Pascal’s triangle.
Let us first find the position of the coefficient by using the general form of any term in the form ${\left( {x + y} \right)^n}$. Any term of the form ${\left( {x + y} \right)^n}$ then it can be written as, ${\left( {x + y} \right)^n} = {x^{n - r}}{y^r}$.
Here for the given problem, $n = 9$ and $r = 4$ substituting this we get
${\left( {x + y} \right)^9} = {x^{9 - 4}}{y^4}$
${\left( {x + y} \right)^9} = {x^5}{y^4}$
Thus, we obtained the position of the coefficient.
Now let us draw Pascal’s triangle.
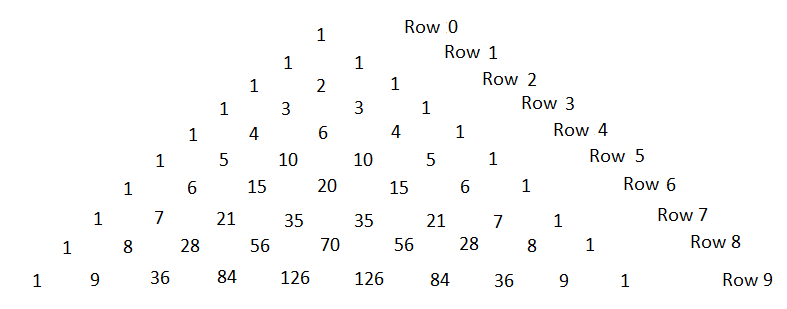
The ninth row of Pascal’s triangle gives us all the coefficients of all the terms in ${\left( {x + y} \right)^9}$ but we need to know the coefficient of the term having the variable ${x^5}{y^4}$. Let us get it from the ninth row of Pascal’s triangle.
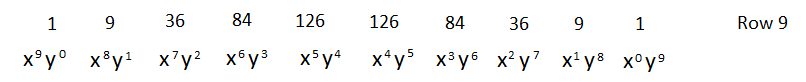
Thus, as we can see the above picture it is clear that the coefficient of the ${x^5}{y^4}$ is $126$ .
Hence, the coefficient of $\left( {\begin{array}{*{20}{c}} 9 \\ 4 \end{array}} \right)$ is $126$.
Note:
In the above problem, one must know how to draw Pascal’s triangle. It starts with the number $1$ that number branches out as two $1's$ after that for the next row we must add these two $1's$ and put it in the next row the sides are filled with ones always this step is repeated until we reach our required row. Here we stopped at the ninth row since the value of $n$ is $9$.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




