
Use graphical method to find the values of k, if (5, k-2) lies on the straight line \[x - 2y + 1 = 0\]
Answer
540.3k+ views
Hint: The general way of solving an equation graphically is as follows:
Firstly we find the value of either of the variables using the given equation. After that for every value of one variable we find the value of the other. Eventually plot the points using the graph table. In the given question, we will keep y on one side and move everything else on the other side of the equation. Then we put the value of x from the given point and find the value of y.
Complete step by step answer:
Now, given equation \[x - 2y + 1 = 0\]
Here, \[y = \dfrac{{x + 1}}{2} - - - - - (1)\]
Let,\[x = 1\] we put this value in equation (1)
We get, \[y = \dfrac{2}{2} = 1\]
Likewise, we put the value of x as 3, 5 and 7.
And find the values of y.
The values of x and y are stated in the table below:
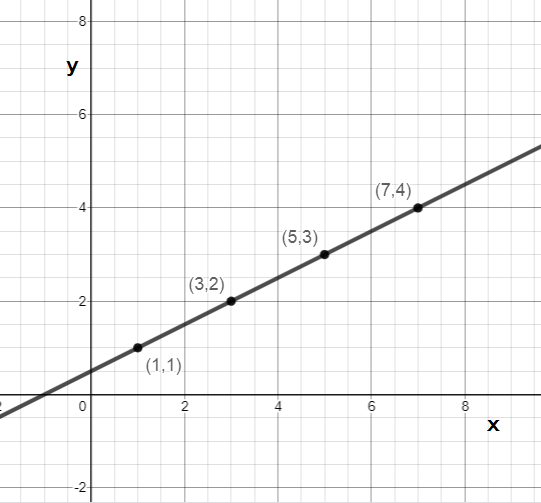
Here, you can see when \[x = 5\]we get \[y = 3\]
Hence, \[k - 2 = 3\]
Therefore, \[k = 5\]which is our required answer.
We plot these point on the graph below:
Note: There are a few things that are to be kept in mind while plotting a graph and assuming values for a variable. Firstly, all the lines drawn on the graph for the purpose of solving the question should be neat and straight always. Second and one the most important thing to keep in mind is that when you assume the values for one the variable make sure they are in regular intervals.
Firstly we find the value of either of the variables using the given equation. After that for every value of one variable we find the value of the other. Eventually plot the points using the graph table. In the given question, we will keep y on one side and move everything else on the other side of the equation. Then we put the value of x from the given point and find the value of y.
Complete step by step answer:
Now, given equation \[x - 2y + 1 = 0\]
Here, \[y = \dfrac{{x + 1}}{2} - - - - - (1)\]
Let,\[x = 1\] we put this value in equation (1)
We get, \[y = \dfrac{2}{2} = 1\]
Likewise, we put the value of x as 3, 5 and 7.
And find the values of y.
The values of x and y are stated in the table below:
| \[x\] | \[1\] | \[3\] | \[5\] | \[7\] |
| \[y\] | \[1\] | \[2\] | \[3\] | \[4\] |
Here, you can see when \[x = 5\]we get \[y = 3\]
Hence, \[k - 2 = 3\]
Therefore, \[k = 5\]which is our required answer.
We plot these point on the graph below:

Note: There are a few things that are to be kept in mind while plotting a graph and assuming values for a variable. Firstly, all the lines drawn on the graph for the purpose of solving the question should be neat and straight always. Second and one the most important thing to keep in mind is that when you assume the values for one the variable make sure they are in regular intervals.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




