Question

Use Euclid’s algorithm to find the H.C.F of $6265$ and $76254$

Answer 1

Hint: In this problem we are asked to find H.C.F of two numbers. Here H.C.F means Highest Common Divisor. When we find all the factors of given two numbers, and some factors are common, then the largest of those common factors is the greatest common factor. So let’s find the H.C.F of given two numbers.

Complete step-by-step solution:
The given terms $6265$ and $76254$,
We have to find H.C.F of the given terms by using Euclid’s algorithm,
Step $1 = $ divided $76254$ by $6265$ and quotient is $12$ and remainder is $1074$.
$76254 = 6265 \times 12 + 1074$
Step $2 = $ remainder is not is not equal to $0$, so again we divided $6265$ by the first remainder is $1074$ and we have a quotient is $5$ and remainder is $895$.
$6265 = 1074 \times 5 + 895$
Step $3 = $ remainder is not equal to zero, so again we divide $1075$ by the second remainder $895$ and we have a quotient of $1$ and remainder is $179$.
$1075 = 895 \times 1 + 179$
Step $4 = $ remainder is equal to zero. So we can stop our process here.
$895 = 179 \times 6 + 0$

Hence, the Highest Common Factor (H.C.F) of numbers $76254$ and $6265$ is $179$.

Additional Information: The Euclidean algorithm, or Euclid’s algorithm, is an efficient method for computing the greatest common divisor of two integers, the largest number that divides them both without a remainder. If G.C.D $\left( {a,b} \right) = 1$ then we say that $a$ and $b$ are co-prime or relatively prime. It is named after the ancient Greek mathematician Euclid, who first described it in his elements.

Note: We can solve this problem by tree factorization method,
The given terms $6265$ and $76254$,

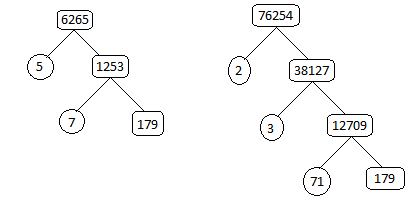
Hence, the Highest Common Factor (H.C.F) of numbers $76254$ and $6265$ is $179$.
The Euclidean Algorithm for finding GCD $\left( {A,B} \right)$ is as follows: If $A = 0$ then the GCD $\left( {A,B} \right) = B$, since the GCD $\left( {0,B} \right) = B$, and we can stop. If $B = 0$ then GCD $\left( {A,B} \right) = A$, since the GCD $\left( {A,0} \right) = A$ and we can stop. Write A in quotient remainder from $\left( {A = B.Q + R} \right)$.