Question

How do you use \[\csc\ \theta = 5\] to find \[\sec(90^{o} - \theta)\] ?

Answer 1

Hint:In this question, we need to find the value of \[\sec(90^{o} - \theta)\] with the use of \[\csc\ \theta = 5\] . Sine , cosine and tangent functions are known as the basic trigonometric functions. Secant function is nothing but a ratio of hypotenuse of the right angle to the adjacent side of the right angle and also a reciprocal of the one of three basic functions. First, we need to consider a right angle triangle ABC, we need to find \[\sec(90^{o} - \theta)\] and \[\text{cosec}\ \theta \]. Thus by equating and simplifying the expression, we can find the value of \[\sec(90^{o} - \theta)\].

Complete step by step answer:
Given, \[\csc\ \theta = 5\]. Here we need to find \[\sec(90^{o} - \theta)\]. We know that secant function is the ratio of the hypotenuse side to the adjacent side.In the triangle, ABC,

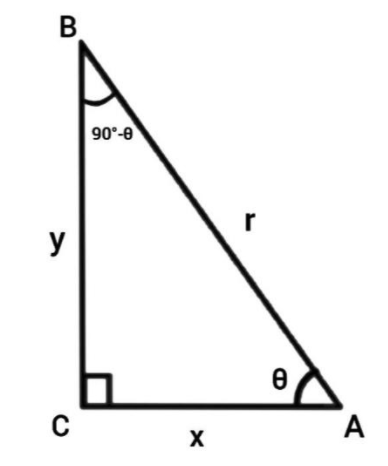
\[\sec\ \theta = \dfrac{\text{hypotenuse}}{\text{adjacent side}}\]
Here \[\theta\] is \[(90^{o} - \theta)\]
\[\sec(90^{o} - \theta) = \dfrac{r}{y}\] ••• (1)
Similarly we know that the Cosecant function is the ratio of the hypotenuse side to the opposite side.
Again in triangle ABC, when \[\theta\] is the angle,
\[\text{cosec}\ \theta = \dfrac{\text{hypotenuse}}{\text{opposite side}}\]
\[\Rightarrow \text{cosec}\ \theta = \dfrac{r}{y}\] •••(2)
Thus on equating (1) and (2) ,
We get,
\[\sec(90^{o} - \theta)\ = \text{cosec}\ \theta\]
Given that \[\text{cosec}\ \theta = 5\]
On substituting the \[{\text{cosec}\theta}\] value,
We get,
\[\sec(90^{o} - \theta)\ = 5\]
Thus the value of \[\sec(90^{o} - \theta)\] is equal to \[5\]

Therefore, the value of \[\sec(90^{o} - \theta)\] is equal to \[5\].

Note:Alternative solution : Given, \[\text{cosec}\ \theta = 5\]. Here we need to find \[\sec(90^{o} - \theta)\]. We know that Cosecant function is the reciprocal of sine function.
\[\text{cosec}\ \theta = 5\]
\[\Rightarrow \dfrac{1}{\sin\theta} = 5\]
Thus \[\sin\ \theta = \dfrac{1}{5}\]
Also we know that secant function is the reciprocal of the cosine function.
\[\sec(90^{o} - \theta)\ = \dfrac{1}{\cos\left( 90^{o} - \theta \right)}\]
We know that \[\cos(90^{o} - \theta) = \sin\ \theta\]
\[\sec\left( 90^{o} - \theta \right) = \dfrac{1}{\sin\theta}\]
By substituting \[\sin\ \theta = \dfrac{1}{5}\], We get,
\[\sec\left( 90^{o} - \theta \right) = \dfrac{1}{\left( \dfrac{1}{5} \right)}\]
On simplifying,
We get,
\[\sec(90^{o} - \theta)\ = \ 5\]
Thus the value of \[\sec(90^{o} - \theta)\] is equal to \[5\].