
How do you use a graphing calculator to find the sum of the geometric series \[\sum{5{{(0.2)}^{n-1}}}\] from n=1 to 10?
Answer
557.7k+ views
Hint: In order to find the solution to this question, we will start by expressing the given expression as a function in terms of n. Then we will write the steps to get the required answer.
Complete step by step answer:
According to the question, we have been asked to find the sum of the geometric series \[\sum{5{{(0.2)}^{n-1}}}\] where the values of n range between 1 to 10.
Now, to solve this, we will first start this question by expressing the equation as a function in terms of n.
Let us consider the function as f(n). Hence, we get the function as
\[f\left( n \right)=\sum{5{{(0.2)}^{n-1}}}\]
Now, to find its final value, we will start by opening the graphing calculator in our device.
As soon as we open our graphing calculator, we follow a few steps to get our answer.
Step 1- We first write the given expression as a function that \[f\left( n \right)=\sum{5{{(0.2)}^{n-1}}}\] in the appropriate place.
Step 2- To write the expression, we will represent ∑ by sum.
Step 3- As we will type sum, a list will appear with 5 options, that are
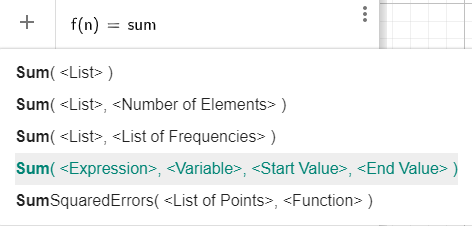
From these 5 options, we will check for the most suitable option according to our given situation.
Step 4- According to our question, we can see the choice 4 will be the more appropriate option to choose, that is Sum(, , , ).
Step 5- Now, we will put the asked value in the chosen option and press the enter key. As soon as we press, we will get our answer.
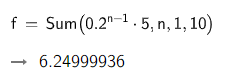
Note:
If we do not want to use a graphing calculator, then we can solve this question, using the formula of the sum of geometric series, that is \[{{S}_{n}}=a\dfrac{({{r}^{n}}-1)}{(r-1)}\]. And then by calculating values of a and r, we will get our answer. And then we can verify our answer using the graphing calculator.
Complete step by step answer:
According to the question, we have been asked to find the sum of the geometric series \[\sum{5{{(0.2)}^{n-1}}}\] where the values of n range between 1 to 10.
Now, to solve this, we will first start this question by expressing the equation as a function in terms of n.
Let us consider the function as f(n). Hence, we get the function as
\[f\left( n \right)=\sum{5{{(0.2)}^{n-1}}}\]
Now, to find its final value, we will start by opening the graphing calculator in our device.
As soon as we open our graphing calculator, we follow a few steps to get our answer.
Step 1- We first write the given expression as a function that \[f\left( n \right)=\sum{5{{(0.2)}^{n-1}}}\] in the appropriate place.
Step 2- To write the expression, we will represent ∑ by sum.
Step 3- As we will type sum, a list will appear with 5 options, that are

From these 5 options, we will check for the most suitable option according to our given situation.
Step 4- According to our question, we can see the choice 4 will be the more appropriate option to choose, that is Sum(
Step 5- Now, we will put the asked value in the chosen option and press the enter key. As soon as we press, we will get our answer.
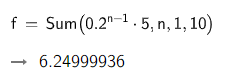
Note:
If we do not want to use a graphing calculator, then we can solve this question, using the formula of the sum of geometric series, that is \[{{S}_{n}}=a\dfrac{({{r}^{n}}-1)}{(r-1)}\]. And then by calculating values of a and r, we will get our answer. And then we can verify our answer using the graphing calculator.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




