
Unit vector \[\widehat{a}\] and \[\widehat{b}\] are inclined at an angle $2\theta $ and \[\left| \widehat{a}-\widehat{b} \right|<1\]. If $0\le \theta <\pi $, then $\theta $ may belong to
(a) $\left[ 0,\dfrac{\pi }{6} \right)$
(b) $\left( \dfrac{\pi }{6},\dfrac{5\pi }{6} \right)$
(c) \[\left[ \dfrac{\pi }{6},\dfrac{\pi }{2} \right]\]
(d) None of these.
Answer
585.6k+ views
Hint: This question is based on the unit vector’s dot product and magnitude concept. In this, we use trigonometric graphs also.
Formula of dot product –
\[\overrightarrow{a}.\overrightarrow{b}=\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\cos \theta \] , where $\theta $is the angle between \[\overrightarrow{a}\]and \[\overrightarrow{b}\].
By using this formula, we get the value of $\left( \widehat{a}.\widehat{b} \right)$ and then by this formula
\[{{\left| \overrightarrow{a}+\overrightarrow{b} \right|}^{2}}={{\left| \overrightarrow{a} \right|}^{2}}+{{\left| \overrightarrow{b} \right|}^{2}}+2\left| \overrightarrow{a}.\overrightarrow{b} \right|\]
We will solve inequality, where we will use the formula –
$\left( {{a}^{2}}-{{b}^{2}} \right)=\left( a+b \right)\left( a-b \right)$
\[\cos 2\theta =2{{\cos }^{2}}-1\]
Complete step by step answer:
Here we use an inequality concept.
Let an inequality - $\left( x-\alpha \right)\left( x-\beta \right)>0$.
To solve, firstly we have to calculate critical points:
$\left( x-\alpha \right)\left( x-\beta \right)=0$
$\Rightarrow x=\alpha $ and $x=\beta $are critical points.
Let $\beta >\alpha $.
So in number line, we have:
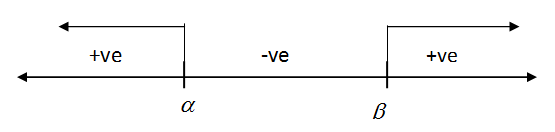
For $x>\beta $, $\left( x-\beta \right)=positive$
$\left( x-\alpha \right)=positive$
So, $\left( x-\alpha \right)\left( x-\beta \right)=positive$
For $\alpha < x<\beta $, $\left( x-\beta \right)=negative$
$\left( x-\alpha \right)=positive$
So, $\left( x-\alpha \right)\left( x-\beta \right)=negative$
For $x<\alpha $, $\left( x-\beta \right)=negative$
$\left( x-\alpha \right)=negative$
$\left( x-\alpha \right)\left( x-\beta \right)=positive$
We have to take $\left( x-\alpha \right)\left( x-\beta \right)=positive$
So, for $x<\alpha $ and $x>\beta $
$\left( x-\alpha \right)\left( x-\beta \right)>0$
So, $x\in \left( -\infty ,\alpha \right)\cup \left( \beta ,\infty \right)$
Now, as given in the question \[\widehat{a}\] and \[\widehat{b}\]are unit vectors and inclined at an angle $2\theta $.
Then, \[\left| \overrightarrow{a} \right|=1\], \[\left| \overrightarrow{b} \right|=1\]and \[\overrightarrow{a}.\overrightarrow{b}=\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\cos 2\theta \]
\[\Rightarrow \overrightarrow{a}.\overrightarrow{b}=\cos 2\theta \]
Now, as given in the question:
\[\left| \widehat{a}-\widehat{b} \right|<1\]
As magnitude of vector is always positive, so we can square both side. So by squaring both sides,
\[{{\left| \widehat{a}-\widehat{b} \right|}^{2}}<1\]
By formula:
\[{{\left| \overrightarrow{a}+\overrightarrow{b} \right|}^{2}}={{\left| \overrightarrow{a} \right|}^{2}}+{{\left| \overrightarrow{b} \right|}^{2}}+2\left| \overrightarrow{a}.\overrightarrow{b} \right|\]
\[\Rightarrow {{\left| \widehat{a} \right|}^{2}}+{{\left| -\widehat{b} \right|}^{2}}+2\left| \widehat{a}.\left( -\widehat{b} \right) \right|<1\]
\[\Rightarrow 1+1-2\left| \widehat{a}.\widehat{b} \right|<1\]
\[\Rightarrow 2-2\left| \widehat{a}.\widehat{b} \right|<1\]
$\because \left| \widehat{a}.\widehat{b} \right|=\cos 2\theta $
\[\Rightarrow 2-2\cos 2\theta <1\]
\[\Rightarrow 2\cos 2\theta >1\]
\[\Rightarrow \cos 2\theta >\dfrac{1}{2}\]
\[\because \cos 2\theta =2{{\cos }^{2}}-1\]
\[\Rightarrow 2{{\cos }^{2}}\theta -1>1\]
\[\Rightarrow 2{{\cos }^{2}}\theta >\dfrac{3}{2}\]
\[\Rightarrow {{\cos }^{2}}\theta >\dfrac{3}{4}\]
\[\Rightarrow {{\cos }^{2}}\theta -\dfrac{3}{4}>0\]
\[\Rightarrow {{\cos }^{2}}\theta -{{\left( \dfrac{\sqrt{3}}{2} \right)}^{2}}>0\]
$\because \left( {{a}^{2}}-{{b}^{2}} \right)=\left( a+b \right)\left( a-b \right)$
\[\Rightarrow \left( \cos \theta +\dfrac{\sqrt{3}}{2} \right)\left( \cos \theta -\dfrac{\sqrt{3}}{2} \right)>0\]
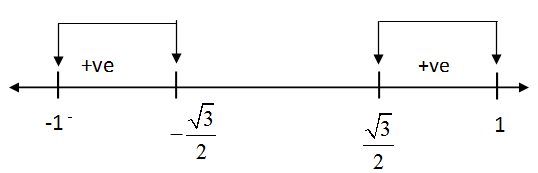
So, $\cos \in \left[ -1,\dfrac{\sqrt{3}}{2} \right)\cup \left( \dfrac{\sqrt{3}}{2},1 \right]$
Graph of $\cos \theta $
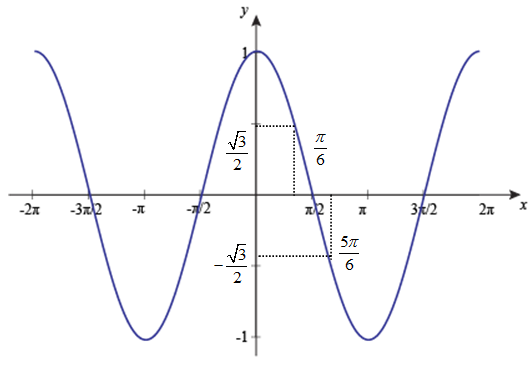
So, according to graph –
$\cos \in \left[ -1,\dfrac{\sqrt{3}}{2} \right)\cup \left( \dfrac{\sqrt{3}}{2},1 \right]$
$\Rightarrow \theta \in \left[ 0,\dfrac{\pi }{6} \right)\cup \left( \dfrac{5\pi }{6},\pi \right]$
Hence, in option (a), $\left[ 0,\dfrac{\pi }{6} \right)$ is correct.
Note:
In this question, students should take care of the inequality signs (< or >) since this can change your answer. So, during calculation especially check this sign is correct or not.
Formula of dot product –
\[\overrightarrow{a}.\overrightarrow{b}=\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\cos \theta \] , where $\theta $is the angle between \[\overrightarrow{a}\]and \[\overrightarrow{b}\].
By using this formula, we get the value of $\left( \widehat{a}.\widehat{b} \right)$ and then by this formula
\[{{\left| \overrightarrow{a}+\overrightarrow{b} \right|}^{2}}={{\left| \overrightarrow{a} \right|}^{2}}+{{\left| \overrightarrow{b} \right|}^{2}}+2\left| \overrightarrow{a}.\overrightarrow{b} \right|\]
We will solve inequality, where we will use the formula –
$\left( {{a}^{2}}-{{b}^{2}} \right)=\left( a+b \right)\left( a-b \right)$
\[\cos 2\theta =2{{\cos }^{2}}-1\]
Complete step by step answer:
Here we use an inequality concept.
Let an inequality - $\left( x-\alpha \right)\left( x-\beta \right)>0$.
To solve, firstly we have to calculate critical points:
$\left( x-\alpha \right)\left( x-\beta \right)=0$
$\Rightarrow x=\alpha $ and $x=\beta $are critical points.
Let $\beta >\alpha $.
So in number line, we have:
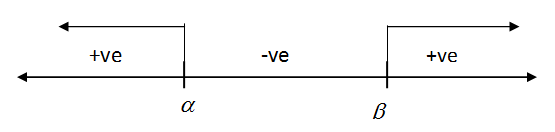
For $x>\beta $, $\left( x-\beta \right)=positive$
$\left( x-\alpha \right)=positive$
So, $\left( x-\alpha \right)\left( x-\beta \right)=positive$
For $\alpha < x<\beta $, $\left( x-\beta \right)=negative$
$\left( x-\alpha \right)=positive$
So, $\left( x-\alpha \right)\left( x-\beta \right)=negative$
For $x<\alpha $, $\left( x-\beta \right)=negative$
$\left( x-\alpha \right)=negative$
$\left( x-\alpha \right)\left( x-\beta \right)=positive$
We have to take $\left( x-\alpha \right)\left( x-\beta \right)=positive$
So, for $x<\alpha $ and $x>\beta $
$\left( x-\alpha \right)\left( x-\beta \right)>0$
So, $x\in \left( -\infty ,\alpha \right)\cup \left( \beta ,\infty \right)$
Now, as given in the question \[\widehat{a}\] and \[\widehat{b}\]are unit vectors and inclined at an angle $2\theta $.
Then, \[\left| \overrightarrow{a} \right|=1\], \[\left| \overrightarrow{b} \right|=1\]and \[\overrightarrow{a}.\overrightarrow{b}=\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\cos 2\theta \]
\[\Rightarrow \overrightarrow{a}.\overrightarrow{b}=\cos 2\theta \]
Now, as given in the question:
\[\left| \widehat{a}-\widehat{b} \right|<1\]
As magnitude of vector is always positive, so we can square both side. So by squaring both sides,
\[{{\left| \widehat{a}-\widehat{b} \right|}^{2}}<1\]
By formula:
\[{{\left| \overrightarrow{a}+\overrightarrow{b} \right|}^{2}}={{\left| \overrightarrow{a} \right|}^{2}}+{{\left| \overrightarrow{b} \right|}^{2}}+2\left| \overrightarrow{a}.\overrightarrow{b} \right|\]
\[\Rightarrow {{\left| \widehat{a} \right|}^{2}}+{{\left| -\widehat{b} \right|}^{2}}+2\left| \widehat{a}.\left( -\widehat{b} \right) \right|<1\]
\[\Rightarrow 1+1-2\left| \widehat{a}.\widehat{b} \right|<1\]
\[\Rightarrow 2-2\left| \widehat{a}.\widehat{b} \right|<1\]
$\because \left| \widehat{a}.\widehat{b} \right|=\cos 2\theta $
\[\Rightarrow 2-2\cos 2\theta <1\]
\[\Rightarrow 2\cos 2\theta >1\]
\[\Rightarrow \cos 2\theta >\dfrac{1}{2}\]
\[\because \cos 2\theta =2{{\cos }^{2}}-1\]
\[\Rightarrow 2{{\cos }^{2}}\theta -1>1\]
\[\Rightarrow 2{{\cos }^{2}}\theta >\dfrac{3}{2}\]
\[\Rightarrow {{\cos }^{2}}\theta >\dfrac{3}{4}\]
\[\Rightarrow {{\cos }^{2}}\theta -\dfrac{3}{4}>0\]
\[\Rightarrow {{\cos }^{2}}\theta -{{\left( \dfrac{\sqrt{3}}{2} \right)}^{2}}>0\]
$\because \left( {{a}^{2}}-{{b}^{2}} \right)=\left( a+b \right)\left( a-b \right)$
\[\Rightarrow \left( \cos \theta +\dfrac{\sqrt{3}}{2} \right)\left( \cos \theta -\dfrac{\sqrt{3}}{2} \right)>0\]
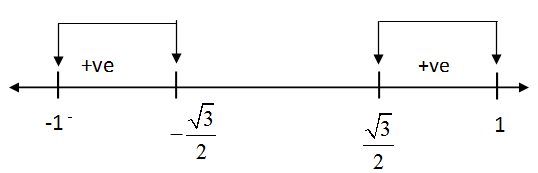
So, $\cos \in \left[ -1,\dfrac{\sqrt{3}}{2} \right)\cup \left( \dfrac{\sqrt{3}}{2},1 \right]$
Graph of $\cos \theta $

So, according to graph –
$\cos \in \left[ -1,\dfrac{\sqrt{3}}{2} \right)\cup \left( \dfrac{\sqrt{3}}{2},1 \right]$
$\Rightarrow \theta \in \left[ 0,\dfrac{\pi }{6} \right)\cup \left( \dfrac{5\pi }{6},\pi \right]$
Hence, in option (a), $\left[ 0,\dfrac{\pi }{6} \right)$ is correct.
Note:
In this question, students should take care of the inequality signs (< or >) since this can change your answer. So, during calculation especially check this sign is correct or not.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
Who Won 36 Oscar Awards? Record Holder Revealed

Who was Subhash Chandra Bose Why was he called Net class 10 english CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

Who is the executive head of the government APresident class 10 social science CBSE

List out three methods of soil conservation

What is the relation between orthocenter circumcentre class 10 maths CBSE




