Question

What is the relation between orthocenter, circumcentre, and centroid?

Answer 1

Hint: First, we shall analyze the given information so that we can able to answer the question. Here, in this question, we are asked to calculate the necessary relation between the orthocenter, the circumcenter, and the centroid of a triangle.

Complete step by step answer:
 The orthocenter of a triangle is nothing but the point where all the three altitudes intersect each other (i.e.) it is the point where the perpendicular drawn from the vertices to the opposite sides of the triangle cut each other.

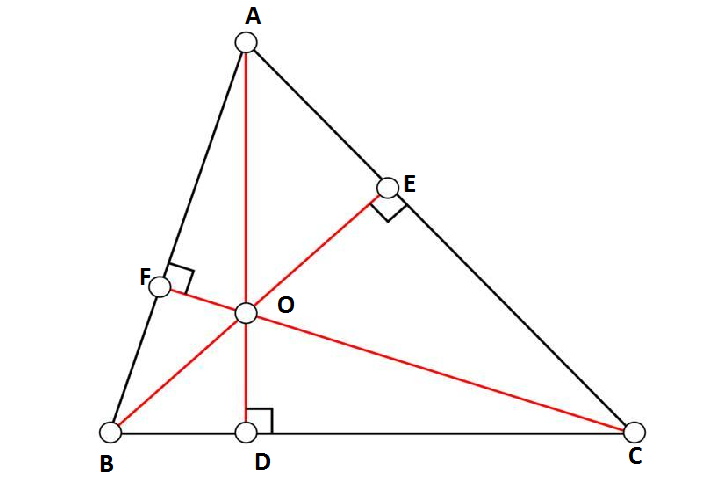
Here the altitudes AD, BE and CF intersect at O. Hence, O is the orthocenter of this triangle.
         The circumcenter of a triangle is nothing but the point where the perpendicular bisectors of the sides of the triangle intersect each other (i.e.) it is the point of concurrency of the bisector of the sides.

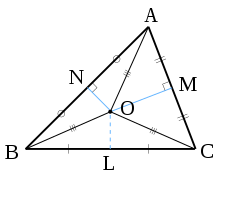
In the above figure, O is the circumcenter of the triangle.
         The centroid of a triangle is nothing but the point where all the three medians of the triangle intersect each other (i.e.) it is the point of intersection of all three medians.

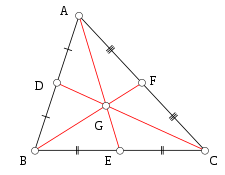
Here the medians AE, BF, and CD intersect at G. Hence, G is the centroid of this triangle.
Here, we are asked to calculate the relation between the orthocenter, circumcenter, and centroid.
Suppose H be the orthocenter, O be the circumcenter and G be the centroid.
Since these three points lie on the same line, these points are said to be the collinear points.
Also, it is a known fact that the centroid divides the orthocenter and the circumcenter internally in the ratio $2:1$
Hence, $\dfrac{{HG}}{{GO}} = 2:1$

Note: From the above explanation, we can understand that when we take an isosceles triangle, the centroid, the orthocenter, and the circumcenter lie on the same line whereas when we take an equilateral triangle, the centroid, the orthocenter, and the circumcenter coincide at a point. This is the required relation between orthocenter, circumcentre, and centroid.