Question

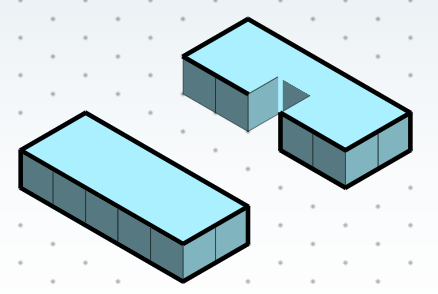
How many unit cubes were removed from the solid on the left to obtain the solid from the right?
A. \[3\]
B. \[4\]
C. \[5\]
D. \[6\]

Answer 1

Hint: Here we will use the formula for finding any number of cubes removed from a figure to form another solid which state as below:
\[{\text{Number of cubes removed}} = \dfrac{{{\text{volume of cuboid removed}}}}{{{\text{volume of one cube}}}}\]

Complete step by step solution:
Step 1: From the above diagram, we can see that both the figures are the same, only some part of the solid one is taken out to obtain the other solid.
Step 2: Now, for calculating the volume of the cuboid removed, we can see from the dots part that the length of the cuboid is \[2\] unit, breadth of the solid is \[1\] unit, and height of the solid is \[2\] unit.
\[ \Rightarrow {\text{Volume of cuboid removed}} = l \times b \times h\]
By substituting the values of length, breadth, and height in the above volume formula, we get:
\[ \Rightarrow {\text{Volume of cuboid removed}} = 2 \times 1 \times 2\]
By multiplying on the RHS side, we get:
\[ \Rightarrow {\text{Volume of cuboid removed}} = 4{\text{ unit cube}}\]
Step 3: Similarly, we will find the volume of one cube. As we know the length, breadth, and height of any smallest cube are equals to \[1\]the unit. So, by using the volume formula, we get:
\[ \Rightarrow {\text{Volume of one cube}} = l \times b \times h\]
By substituting the values of length, breadth, and height in the above volume formula, we get:
\[ \Rightarrow {\text{Volume of one cube}} = 1 \times 1 \times 1\]
By multiplying on the RHS side, we get:
\[ \Rightarrow {\text{Volume of one cube}} = 1{\text{ unit cube}}\]
Step 4: Now, by using the formula for finding the number of cubes removed from the solid, we get:
\[{\text{Number of cubes removed}} = \dfrac{{4{\text{ unit cube}}}}{{{\text{1 unit cube}}}}\]\[\left( {\because {\text{volume of cuboid removed}} = 4{\text{ unit cube & volume of one cube}} = 1{\text{ unit cube}}} \right)\]
By dividing into the RHS side in the above formula, we get:
\[{\text{Number of cubes removed}} = 4\]

\[\therefore \]\[{\text{Number of cubes removed}} = 4\]

Note: In these types of questions students need to take care while calculating the volume of the removed part of the solid. You should also remember that a cube is a three-dimensional solid object which is bounded by six square faces or we can say sides. So, the volume of any smallest cube possible will be equal \[1{\text{ unit cube}}\].