Question

What type of dilation is determined by a scale factor of $\dfrac{2}{3}$?

Answer 1

Hint: For solving this type of question you should know what is dilation and what is the process for doing it. We can say that the dilation is a transformation that changes the size of a figure. The dilation is also known as similarity transformation. And it is completely dependent on scale factor $k$.

Complete step-by-step solution:
According to our question it is asked what type of dilation is determined by a scale factor of $\dfrac{2}{3}$. Actually, we know that the dilation is a transformation that changes the size of a figure and it requires a centre point and a scale factor $k$.

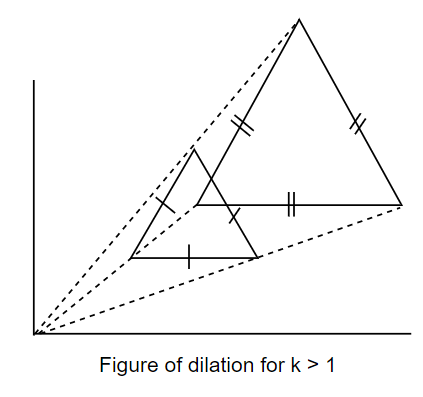
In the figure, the original object is the one with a single mark on its sides and the enlarged or reduced figure is the one with double mark on its sides. According to the figures it is clear that the dilation can be of two types:
(1) Enlargement
(2) Reduction
Enlargement: It is a type of dilation which will take place when $\left| k \right|>1$, in this dilation the new figure after the dilation will be greater than the old figure or original figure. And it will be bigger than that figure in a fixed ratio to that, as if we reduce it with the same ratio, then it will be again the same as the old figure.
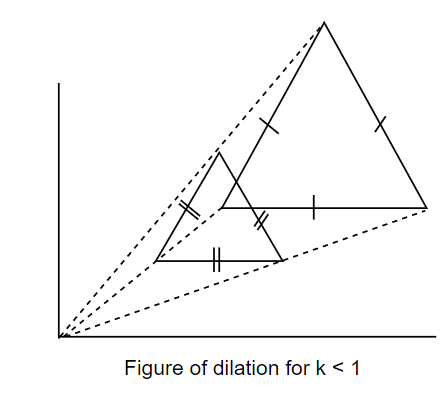
Reduction: It is a type of dilation which will take place when $\left| k \right|<1$, in this dilation the new figure after the dilation will be less than the original figure. And it will be smaller than that figure in a fixed ratio as if we increase it with the same ratio, then it will be again as same as the old figure.
So, if we see our question then the scale factor $k$ is:
$\begin{align}
  & k=\dfrac{2}{3} \\
 & \left| k \right|=\left| \dfrac{2}{3} \right|<1 \\
\end{align}$
Here, $\left| k \right|<1$, so it will be a reduction (contraction) dilation in this. And it will be smaller by a factor of 66.67%.

Note: During the solving of this question, you should be careful of the ratio of the original figure and the new figure because if our dimensions or points of centre will be disturbed then the figure will not be in the same shape as the old figure. And we have to be careful about the scale factor because this decides the contraction and enlargement.