Question

Two-point masses of 0.3kg and 0.7kg are fixed at the ends of a rod of length 1.4m and of negligible mass. The rod is set rotating about an axis perpendicular to its length with a uniform angular speed. The point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum is located at a distance of
A.0.42m from the mass of 0.3kg
B.0.70m from the mass of 0.7kg
C.0.98m from the mass of 0.3kg
D.0.98m from the mass of 0.7kg

Answer 1

Hint: From the work-energy theorem we know that the net work done by all the forces on an object will be equal to the change in its kinetic energy, and the kinetic energy is dependent on the moment of inertia and the angular velocity of the rod which is rotation.

Complete answer:
Here it is given that the angular velocity is constant so the kinetic energy will be dependent only on the inertia and work done to rotate the rod will be dependent on the kinetic energy so indirectly the work done is dependent on the moment of inertia of the body. So, for the work to be done to be minimum the moment of inertia for the rod must be minimum.
Let us assume that the required point is $O$. And from the given conditions we will draw a diagram which shows the exact condition which is given in the question. So, the diagram is as follows,

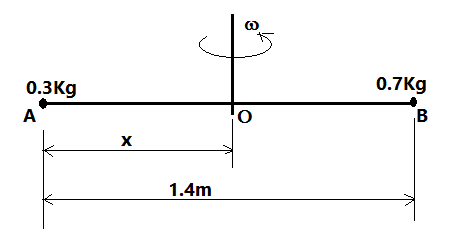
Given that the mass of the rod is negligible.
From the work energy theorem,
${W_{all forces}} = \dfrac{1}{2}I{\omega ^2}$, where $\omega $ is constant, so the ${W_{all forces}}$ will be minimum when $I$ will be minimum.
So now we will write the expression for the moment of inertia.
Let the point $O$is at the distance of $x$ from one end, then the moment of inertia,
$I = 0.3 \times {(x)^2} + 0.7 \times {(1.4 - x)^2}$
Now $I$ is to be minimum so the differentiation will be zero for $I$ to be minimum.
So, $\dfrac{{dI}}{{dx}} = 0$
$\dfrac{d}{{dx}}\left[ {0.3 \times {{(x)}^2} + 0.7 \times {{(1.4 - x)}^2}} \right] = 0$
$ \Rightarrow 0.3 \times 2x - 0.7 \times 2(1.4 - x) = 0$
$ \Rightarrow 0.6x - (0.7 \times 2.8) + (0.7 \times 2x) = 0$
$ \Rightarrow 0.6x - 1.96 + 1.4x = 0$
$ \Rightarrow 2x = 1.96$
$ \Rightarrow x = \dfrac{{1.96}}{2}$
$ \Rightarrow x = 0.98m$
So, the point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum is located at a distance of $0.98m$ from the mass of 0.3kg

Hence, option (C) is the correct answer.

Note:
Here we have seen the role of the work-energy theorem and we came to know that the work-energy theorem is useful in the analysing of the situations where a rigid body moves under several forces. The rigid body only possesses the kinetic energy since a rigid body cannot store a potential energy due to its rigid structure. This is the reason because of which the work done by any force acting on the rigid body is equal to the change in the kinetic energy.