Question

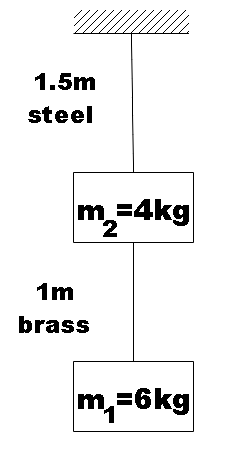
Two wires of diameter 0.25cm, one made of steel and the other made of brass are loaded as shown in Fig. The unloaded length of steel wire is 1.5 m and that of brass wire is 1m. Compute the elongations of the steel and the brass wires. Given young’s modulus of steel = $2\times {{10}^{-11}}Pa$ and that of brass is $0.9\times {{10}^{-11}}Pa$.

Answer 1

Hint: We have to use the formula for Young's modulus to solve this question. Calculate the stress in both the wires by finding the value of tension and dividing it by the cross sectional area of wire. To calculate the tensions equate the net forces on the both to zero. Substitute the values in the formula of Young's modulus and find the elongation.

Formula used:
$Y=\dfrac{stress}{strain}$
$stress=\dfrac{F}{A}$
$strain=\dfrac{\Delta l}{l}$
F=mg

Complete answer:
It is given that the two wires of same diameter of 0.25cm are loaded as shown. The length of the steel and the brass wires are given to be 1.5m and 1m respectively.
Also, the young’s moduli of both wires are given and we are supposed to find the elongations in both of the wires.
To find the elongations of both the wires, we will use the formula for young’s modulus of a given body.
Young’s modulus is defined as the ratio of stress in the body to the strain in the body.
That is,
$Y=\dfrac{stress}{strain}$
Stress is equal to the perpendicular force (F) exerted on the body per unit area of the surface on which it is acting.
That is,
$stress=\dfrac{F}{A}$
In case of a wire, the force is equal to the tension in the wires and area is equal to its cross sectional area.
Strain is equal to the ratio of the change in length (elongation) of the body to the original length (l).
$strain=\dfrac{\Delta l}{l}$.
This means that $Y=\dfrac{\dfrac{F}{A}}{\dfrac{\Delta l}{l}}=\dfrac{F\Delta l}{Al}$ …. (i).
Therefore, let us apply equation (i) for both the wires and find the elongation in both i.e. $\Delta l$
Let first consider the brass wire.

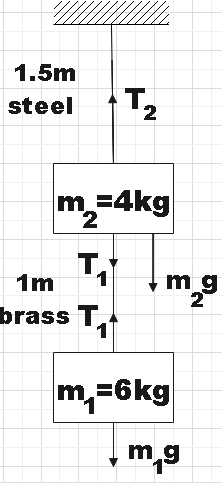
The load on this wire is 6kg. We know that this block is at rest. That means that the tension (${{T}_{1}}$) in the string is equal to the gravitational force (${{F}_{1}}$) on this block.
$\Rightarrow {{T}_{1}}={{F}_{1}}$
Gravitational force on a body of mass is given as$F=mg$, where m is the mass of the body and g is acceleration due to gravity.
$\Rightarrow {{F}_{1}}=(6)(9.8)=58.8N$
$\Rightarrow {{T}_{1}}={{F}_{1}}=58.8N$
The cross sectional area of the brass wire will be
 \[{{A}_{1}}=\pi {{\left( \dfrac{d}{2} \right)}^{2}}\]
Where, s is the diameter.
It is given d = $0.25cm=25\times {{10}^{-4}}m$
\[{{A}_{1}}=\pi {{\left( \dfrac{25\times {{10}^{-4}}}{2} \right)}^{2}}\].
The original length of this wire is ${{l}_{1}}=1m$
The young’s modulus of brass is${{Y}_{1}}=0.9\times {{10}^{-11}}Pa$.
Substitute all the known values in equation (i).
$\Rightarrow 0.9\times {{10}^{-11}}=\dfrac{58.8(\Delta l)}{\pi {{\left( \dfrac{25\times {{10}^{-4}}}{2} \right)}^{2}}.1}$
$\Rightarrow \Delta l=\dfrac{0.9\times {{10}^{-11}}\times \pi {{\left( \dfrac{25\times {{10}^{-4}}}{2} \right)}^{2}}}{58.8}=1.3\times {{10}^{-4}}m$.
This means that the elongation in the brass wire is $1.3\times {{10}^{-4}}m$.
In case of the steel wire, the net force on the 4kg block is ${{T}_{2}}-{{m}_{2}}g-{{T}_{1}}$. And the net force on this block is also zero.
$\Rightarrow {{T}_{2}}-{{m}_{2}}g-{{T}_{1}}=0$.
$\Rightarrow {{T}_{2}}-(4)(9.8)-(58.8)=0$
$\Rightarrow {{T}_{2}}=98N$
The area of the cross section of steel wire will equal to that of the brass wire as they both have the same diameter.
\[\Rightarrow {{A}_{2}}=\pi {{\left( \dfrac{25\times {{10}^{-4}}}{2} \right)}^{2}}\].
${{l}_{2}}=1.5m$.
${{Y}_{2}}=2\times {{10}^{-11}}Pa$.
Substitute the values in equation (i).
$\Rightarrow 2\times {{10}^{-11}}=\dfrac{98(\Delta l)}{\pi {{\left( \dfrac{25\times {{10}^{-4}}}{2} \right)}^{2}}(1.5)}$
$\Rightarrow \Delta l=\dfrac{2\times {{10}^{-11}}\times \pi {{\left( \dfrac{25\times {{10}^{-4}}}{2} \right)}^{2}}(1.5)}{98}=1.49\times {{10}^{-4}}m$
This means that the elongation in the steel wire is $1.49\times {{10}^{-4}}m$.

Note:
Some students may make a mistake in calculating the tension in the steel wire. They may make the mistake by considering the net force of the load of mass 4kg as ${{T}_{2}}-{{m}_{2}}g$ and forget the tension force exerted by the brass wire.