Question

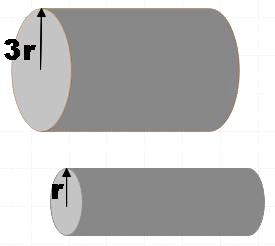
Two wire segments are shown; both are made of the same material and are a part of a larger circuit and have an electric field E across its length. However, one has a larger cross-sectional surface area, due to the radius being 3x that of the skinnier wire. Which is true?
1. The large wire has a greater charge density.
2. The larger wire has a greater current.
3. The larger wire has low resistance.

A. 1 only
B. 2 only
C. 3 only
D. 1 and 2

Answer 1

Hint: As there is a possibility of multiple answers being true, we have to approach all the given statements one by one. Remember that current density is a material dependent property. Also, for statement 2, assume that the given wires are a part of a larger circuit in which all connections are made in series. Now for statement 3, recall the expression for resistance and hence, answer the question.

Formula used:
Resistance,
$R=\rho \dfrac{l}{\pi {{r}^{2}}}$

Complete step-by-step answer:
In the question, we are given two segments of wire that are made of the same material. Both these segments form a part of a larger circuit and have an electric field of E across its length. We are also said that one of the segments has a larger cross-sectional area with three times the radius of the other. These conditions are followed by three statements and we are asked to find the correct statement among them.
Statement 1: The large wire has a greater charge density.
We know that charge density is independent of the dimensions of the wire and is a property of the material. Since both the given wire segments are said to be of the same material, both will have the same current density and hence statement 1 is found to be false.
Statement 2: The larger wire has a greater current.
For the same circuit, assuming all the connections are made in series, the current will be across all the wire. Here as both wires form a part of a larger circuit, the current will be the same for both. Hence, statement 2 is also false.
Statement 3: The larger wire has low resistance.
Let us recall the expression for resistance,
$R=\rho \dfrac{l}{A}$
Where, A is the area of cross section of the wire given by,
$A=\pi {{r}^{2}}$
$\Rightarrow R=\rho \dfrac{l}{\pi {{r}^{2}}}$
Clearly, resistance is inversely proportional to the square of the radius of the wire. Hence, larger wire will have lower resistance than the other. Therefore, statement 3 is true.
As only the third statement is true, option C is the right answer.

So, the correct answer is “Option C”.

Note: You may have noted that in the case of statement 2, we have specified to assume all the connections to be in series. This is because, in case of branching, as per Kirchoff’s junction rule, the current entering the junction should be equal to the current leaving the junction. So, the current will be different for different branches.