Question

Two wheels $1$ and $2$ of radii ${r_1}$ and ${r_2}$ are connected by a belt. If the belt does not slip on the wheels and angular speed of wheel $1$ is $\omega $ then acceleration of P relative to Q is

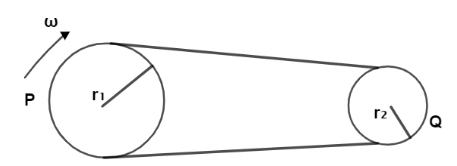
A. ${r_1}{\omega ^2}(1 + \dfrac{{{r_2}}}{{{r_1}}})$
B. ${r_1}{\omega ^2}(1 + \dfrac{{{r_1}}}{{{r_2}}})$
C. ${r_1}{\omega ^2}$
D. ${r_1}{\omega ^2}(1 + \dfrac{{{r_2}}}{{{r_2}^2}})$

Answer 1

Hint: In order to solve this problem we need to understand angular acceleration which states that angular acceleration is the time derivative of angular velocity whereas angular velocity is the time derivation of angle which body rotates in some period.On a moving body around the axis each particle has its velocity along the tangent and it is equal to the product of angular velocity and radius in which it is moving.

Complete step by step answer:
Here we use formulas of angular velocity and angular acceleration.
Let $\omega $ be angular velocity and “v” be its speed.
Then from relation $v = r\omega $ for the first wheel is $v = {r_1}\omega $.
And for second let it rotates with angular velocity ${\omega _2}$ so using relation of speed we get
$v = {r_2}{\omega _2}$
Equating both speed we get ${r_1}\omega = {r_2}{\omega _2}$
\[ \Rightarrow {\omega _2} = \dfrac{{{r_1}\omega }}{{{r_2}}}\]
We know from relativity that ${\vec \alpha _{PQ}} = {\vec \alpha _P} - {\vec \alpha _Q}$
Where $\alpha $ is angular acceleration

Also using $\alpha = r{\omega ^2}$
We get ${\vec \alpha _p} = {r_1}{\omega ^2}\hat i$ and ${\vec \alpha _Q} = - {r_2}{\omega _2}^2\hat i$
Using value of ${\omega _2}$ we get ${\vec \alpha _Q} = {r_2}(\dfrac{{{r_1}^2{\omega ^2}}}{{{r_2}^2}})\hat i$
$ \Rightarrow {\vec \alpha _Q} = - \dfrac{{{r_1}^2{\omega ^2}}}{{{r_2}}}\hat i$
$\Rightarrow {\vec \alpha _{PQ}} = {r_1}{\omega ^2}\hat i + \dfrac{{{r_1}^2{\omega ^2}}}{{{r_2}}}\hat i$
$\therefore {\vec \alpha _{PQ}} = {r_1}{\omega ^2}\left[ {1 + \dfrac{{{r_1}}}{{{r_2}}}} \right]\hat i$

So the correct option is B.

Note: It should be remembered that the direction of angular acceleration of Q is opposite to that of P because due to belt wrapping Q the wheel moves in the opposite direction so that belt is stationary. If both moves in the same direction then the belt starts moving due to the same directional force applied on it and hence our calculation goes wrong. Also when second wheel motion is analyzed with respect to first the second wheel is assumed to be at rest.