Question

Two vertices of a triangle are $\left( 1,3 \right)$ and $\left( 4,7 \right)$ .The orthocentre lies on the line $x+y=3$ . The locus of the third vertex is:
A. ${{x}^{2}}-2xy+2{{y}^{2}}-3x-4y+36=0$
B. $2{{x}^{2}}-4xy+3{{y}^{2}}-4x-y+42=0$
C. $3{{x}^{2}}+xy-4{{y}^{2}}-2x+24y-40=0$
D. ${{x}^{2}}-4xy+3{{y}^{2}}-2x-y+40=0$

Answer 1

Hint: Orthocentre is the point of intersections of perpendiculars drawn from vertex to the opposite side of the triangle.
Equation of line with slope $m$ and passing through $\left( {{x}_{1}},{{y}_{1}} \right)$ is given as $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$ .

Complete step by step solution:
Let $PQR$ be the given triangle and $P=\left( h,k \right)$ be the vertex whose locus is to be found.
In the question it is given that the co-ordinates of vertex $Q$ are $\left( 1,3 \right)$ and the co-ordinates of vertex $R$ are $\left( 4,7 \right)$ .

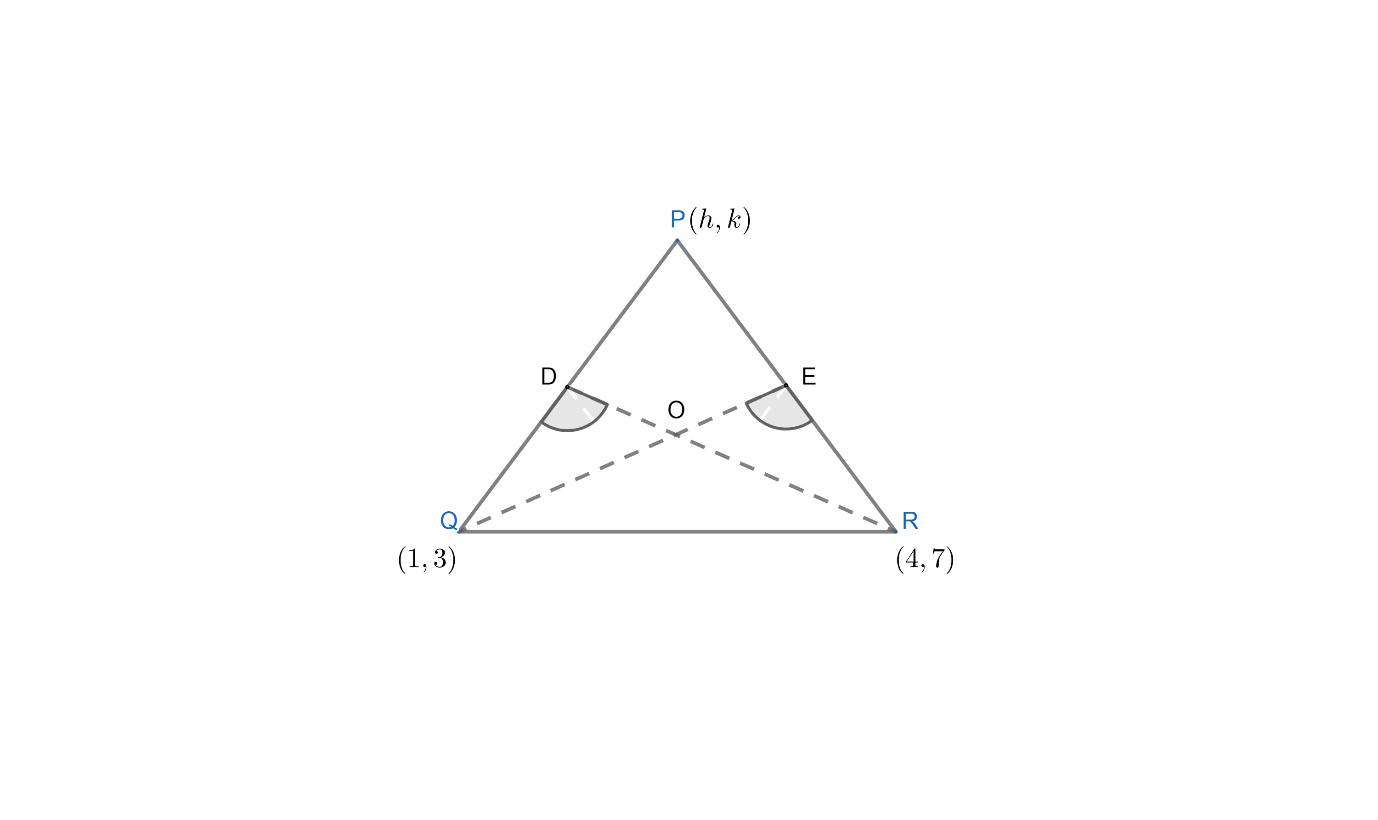
Let the coordinates of the orthocentre be $\left( {{x}_{1}},{{y}_{1}} \right)$ . Now , from the question we can conclude that $\left( {{x}_{1}},{{y}_{1}} \right)$ satisfy the equation $x+y=3$ .
So, ${{x}_{1}}+{{y}_{1}}=3$
$\Rightarrow {{y}_{1}}=3-{{x}_{1}}$
So , the coordinate of the orthocentre becomes $\left( {{x}_{1}},3-{{x}_{1}} \right)$ .
Now , consider the figure.
Since $O$ is the orthocentre , so $RE\bot QE$ . Now, Q, O and E are collinear. So, the slope of line QE is equal to slope of line QO. Also, R, E and P are collinear. So, slope of RP = slope of RE. RD is perpendicular to QP. R, O and D are collinear. So, slope of RO = slope of RD. Also, Q, D and P are collinear. So, slope of QD = slope of QP.

Now , we know , the slope of the line joining two points \[({{x}_{1}},{{y}_{1}})\] and \[({{x}_{2}},{{y}_{2}})\] is given as \[m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\].
So, the slope of QE = slope of $QO=\dfrac{3-{{x}_{1}}-3}{{{x}_{1}}-1}=\dfrac{{{x}_{1}}}{1-{{x}_{1}}}$ and the slope of RD = slope of RO = $\dfrac{7-\left( 3-{{x}_{1}} \right)}{4-{{x}_{1}}}=\dfrac{4+{{x}_{1}}}{4-{{x}_{1}}}$ .
We know that if two lines are perpendicular to each other , then the product of their slopes is equal to \[-1\] .
So , slope of RE \[\times \] slope of QE = -1
$\Rightarrow $ Slope of RE \[\times \dfrac{{{x}_{1}}}{1-{{x}_{1}}}=-1\]
$\Rightarrow $ Slope of RE $=\dfrac{{{x}_{1}}-1}{{{x}_{1}}}$
Also, $QD\bot RD$ .
So, slope of $QD\times $ slope of $RD=-1$
$\Rightarrow $ Slope of QD $\times \dfrac{4+{{x}_{1}}}{4-{{x}_{1}}}=-1$
\[\Rightarrow \] Slope of QD \[=\dfrac{{{x}_{1}}-4}{{{x}_{1}}+4}\]
Now, let’s find the equation of $PE\And PD$ .
We know, equation of line with slope $m$ and passing through $\left( {{x}_{1}},{{y}_{1}} \right)$ is given as $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$ .
So, equation of $PE$ is given as $\left( y-7 \right)=\dfrac{{{x}_{1}}-1}{{{x}_{1}}}\left( x-4 \right)$ .
[We take ${{x}_{1}}$ and ${{y}_{1}}$ as $\left( 4,7 \right)$ because $PE$ passes through $R\left( 4,7 \right)$ .]
$\begin{align}
  & \Rightarrow {{x}_{1}}\left( y-7 \right)={{x}_{1}}\left( x-4 \right)-x+4 \\
 & \Rightarrow {{x}_{1}}\left( y-x-3 \right)=-\left( x-4 \right).........\left( i \right) \\
\end{align}$
Now, equation of $PD$ is given as $\left( y-3 \right)=\dfrac{{{x}_{1}}-4}{{{x}_{1}}+4}\left( x-1 \right)$ .
[$PD$ passes through $Q\left( 1,3 \right)$ .]
$\begin{align}
  & \Rightarrow {{x}_{1}}\left( y-3 \right)+4\left( y-3 \right)={{x}_{1}}\left( x-1 \right)-4\left( x-1 \right) \\
 & \Rightarrow {{x}_{1}}\left( y-x-2 \right)=-\left( 4y+4x-16 \right)............\left( ii \right) \\
\end{align}$
Now, the vertex $P\left( h,k \right)$ satisfies both equations $\left( i \right)\And \left( ii \right)$ .
So, equation $\left( i \right)$ becomes ${{x}_{1}}\left( k-h-3 \right)=-\left( h-4 \right).........\left( iii \right)$
And equation $\left( ii \right)$ becomes ${{x}_{1}}\left( k-h-2 \right)=-\left( 4k+4h-16 \right).......\left( iv \right)$
Now, on dividing equation $\left( iii \right)\And \left( iv \right)$ , we get;
$\dfrac{{{x}_{1}}\left( k-h-3 \right)}{{{x}_{1}}\left( k-h-2 \right)}=\dfrac{-\left( h-4 \right)}{-\left( 4k+4h-16 \right)}$
$\begin{align}
  & \Rightarrow \left( k-h-3 \right)\left( 4k+4h-16 \right)=\left( h-4 \right)\left( k-h-2 \right) \\
 & \Rightarrow 4{{k}^{2}}+4kh-16k-4kh-4{{h}^{2}}+16h-12k-12h+48=kh-{{h}^{2}}-2h-4k+4h+8 \\
 & \Rightarrow 4{{k}^{2}}-3{{h}^{2}}-hk+2h-24k+40=0........(v) \\
\end{align}$
Now, to find the locus of \[P\left( h,k \right)\] , we will substitute \[(x,y)\] in place of \[\left( h,k \right)\] in equation \[(v)\] .
So, the locus of $P\left( h,k \right)$ is given as $4{{y}^{2}}-3{{x}^{2}}-xy+2x-24y+40=0$ .
$\Rightarrow 3{{x}^{2}}-4{{y}^{2}}+xy-2x+24y-40=0$
Hence, the locus of P is given by the equation $3{{x}^{2}}-4{{y}^{2}}+xy-2x+24y-40=0$ .
Hence, the correct option is option (c) .

Note: While simplifying the equation take care of sign of terms. These equations can be confusing and sign mistakes are very common. Don’t get confused with orthocenter and circumcentre.