Question

Two vertices of a triangle are \[(0,2)\] and \[(4,3)\]. If its orthocenter is at the origin, then its third vertex lies in which quadrant?
A. Fourth
B. Second
C. Third
D. First

Answer 1

Hint: We must assume the third vertex as \[(h,k)\], write equation of any two altitudes through two vertices, which should be of the form \[y - {y_1} = m\left( {x - {x_1}} \right)\]. Since orthocenter is the point of intersection of these two lines i.e. altitudes so it satisfies both these equations. This gives two equations in h and k, which generally looks like \[mh + nk = p\] where m, n, p are constants. If we solve them it will give actual coordinates i.e. \[(h,k)\] of the third vertex.

Complete step by step answer:
Orthocenter of a triangle is the point of intersection of altitudes of the triangle.
Let us assume the coordinates of the third vertex to be \[(h,k)\],

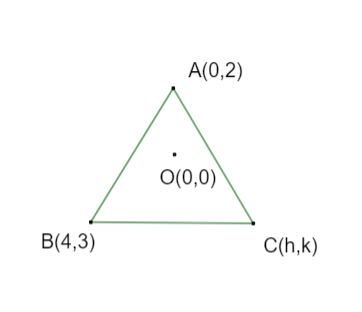
Now to find the slope of line perpendicular to AB, we use method given below –
To find the slope (m) of a line having two points \[\left( {{x_1},{y_1}} \right)\] and \[\left( {{x_2},{y_2}} \right)\] we use given formula,
\[m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\]
Hence, slope of AB can be determined by using above formula where slope is denoted by \[{m_{AB}}\] :–
Since coordinates of A and B are \[\left( {0,2} \right)\] and \[\left( {4,3} \right)\] respectively,
\[{m_{AB}} = \dfrac{{3 - 2}}{{4 - 0}}\]
\[{m_{AB}} = \dfrac{1}{4}\]
We have a unique relation between slopes \[m\] and \[{m_ \bot }\] of two perpendicular lines i.e.
\[m \times {m_ \bot } = - 1\]
Now we use this relation to find slope of line perpendicular to AB denoted by,
\[{m_{AB}} \times {m_{ \bot AB}} = - 1\]
\[{m_{ \bot AB}} = \dfrac{{-1}}{\dfrac{1}{4}}\]
\[{m_{ \bot AB}} = - 4\]
Slope of AC denoted as \[{m_{AC}}\] can also be found using the slope-formula stated above –
Using the coordinates of A and B i.e., \[\left( {0,2} \right)\] and \[\left( {h,k} \right)\]respectively in order to find the slope using the same slope formula stated above:
\[{m_{AC}} = \dfrac{{k - 2}}{h}\]
Similarly we can write the relation stated above to find the slope of line perpendicular to AC:
\[{m_{AC}} \times {m_{ \bot AC}} = - 1\]
\[{m_{ \bot AC}} = \dfrac{{ - 1}}{{\dfrac{{k - 2}}{h}}}\]
\[{m_{ \bot AC}} = \dfrac{h}{{2 - k}}\]
 As we know that the equation of a line passing through a point \[(x',y')\] with slope \[m\] is given by:
\[y - y' = m(x - x')\]
Similarly, the equation of a line perpendicular to line AC is given below as:
\[y - 3 = \dfrac{h}{{2 - k}}(x - 4)...(1)\]
And the equation of line perpendicular to line AB is given below as:
\[y - k = - 4(x - h) \ldots (2)\]
Since orthocenter is intersection of \[(1)\] and \[(2)\], and its value is already mentioned in question as $\left( {0,0} \right)$,
We put \[(0,0)\] in both equations, since orthocenter satisfies $\left( 1 \right)$ and $\left( 2 \right)$
First we put values of \[x = 0,y = 0\] in equation $\left( 1 \right)$,
\[0 - 3 = \dfrac{h}{{2 - k}}(0 - 4)\]
\[ - 3 = \dfrac{{ - 4h}}{{2 - k}}\]
\[3(2 - k) = 4h\]
\[4h + 3k = 6....(3)\]
Again we put \[x = 0,y = 0\] in second equation $\left( 2 \right)$,
\[0 - k = - 4(0 - h)\]
\[ - k = - 4 \times - h\]
\[k = - 4h\]
Using both relations
\[(h,k) = \left( { - \dfrac{3}{4},3} \right)\]

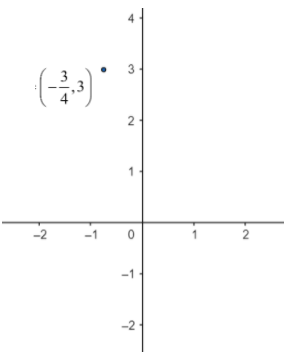
So, the correct answer is “Option B”.

Note: The student must have an idea of what an orthocenter is and also to write equations of line passing through two points and its slope given as \[y - y' = m(x - x')\]. The student must be able to identify origin and know how to locate a point on the graph.