Question

Two vertical poles of heights 20m and 80m stand 50m apart on a horizontal plane. The height (in m) of the point of intersection of the lines joining the top of each pole to the foot of the other, from this horizontal plane is
A. 15m
B. 16m
C. 18m
D. 50m

Answer 1

Hint: Use basic proportionality theorem, if two triangles are similar then the ratio of their alternate sides will be equal. In order to solve this first we have considered the figure as shown below then we have equated their alternate side ratio of the triangles formed in order to find the value of a as represented in the figure.

Complete step-by-step answer:

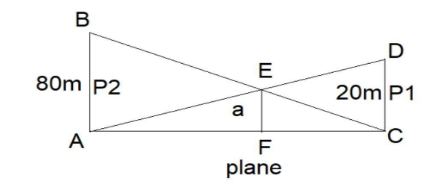
Let us consider a triangle ABC and ADC intersecting at a point E as shown in the figure
Let the height of the point of intersection of the lines joining the top of each pole to the foot of the other, from this horizontal plane be represented by EF.
According to initial data we have
AB=80m
CD=20m
 AC=50m
It is clear that AB, EF AND CD are perpendiculars on the line AC from figure
Since all are perpendicular to AC, therefore AB||CD||EF
Now let us consider the triangle ABC & triangle EFC,
Using basic proportionality theorem we have
\[\dfrac{{AC}}{{AB}} = \dfrac{{FC}}{{FE}}\]
On substituting the values we have
\[\dfrac{{AC}}{{80}} = \dfrac{{FC}}{a}\]
$FC = a \times \dfrac{{AC}}{{80}}...........(1)$
Similarly in triangle DCA & triangle EFA
Using basic proportionality theorem we have
\[\dfrac{{AC}}{{DC}} = \dfrac{{AF}}{{EF}}\]
On substituting the values we have
\[\dfrac{{AC}}{{20}} = \dfrac{{AF}}{a}........(2)\]
From figure we know that
\[AF = AC - FC........(3)\]$
    \\
    \\
 $
From (1), (2) and (3) we have
$\dfrac{{AC}}{{20}} = \dfrac{{AC - (\dfrac{{aAC}}{{80}})}}{a}$
Eliminating AC from above equation we get
$\dfrac{1}{{20}} = \dfrac{{1 - (\dfrac{a}{{80}})}}{a}$
On simplifying we have
$
  \dfrac{a}{{20}} = \dfrac{{80 - a}}{{80}} \\
  a = 20 - \dfrac{a}{4} \\
 $
On taking $\dfrac{a}{4}$ on left side we get
$
  a + \dfrac{a}{4} = 20 \\
  \dfrac{{4a + a}}{4} = 20 \\
 $
On further solving we get
$5a = 80$
Finally we get
$a = 16$
Therefore the height (in m) of the point of intersection of the lines joining the top of each pole to the foot of the other, from this horizontal plane is 16 m.

Hence option (B) is the correct answer.

Note: For the height and distance questions just stick with the basic trigonometric formulas and similar triangle properties. Make sure you make a correct diagram and try to find the solution in the diagram itself. Always consider the right triangle in order to get the value easily, try to make less equations in order to solve the problem.