Question

When two vectors of magnitudes $P$ and $Q$ are inclined at an angle $\theta $, the magnitude of their resultant is $2P$. When the inclination is changed to ${{180}^{0}}-\theta $, the magnitude of the resultant is halved. Find the ratio of $P$ to $Q$.

Answer 1

Hint: This problem can be solved by using the cosine law for the magnitude of the resultant of two vectors. By plugging in the information given in the question in the form of two equations and comparing them, we can get the required ratio.
Formula used:

The magnitude $\left| \overrightarrow{R} \right|$ of the resultant $\overrightarrow{R}$ of two vectors $\overrightarrow{A}$ and $\overrightarrow{B}$ is given by

$\overrightarrow{\left| R \right|}=\sqrt{{{\overrightarrow{\left| A \right|}}^{2}}+{{\overrightarrow{\left| B \right|}}^{2}}+2\overrightarrow{\left| A \right|}\overrightarrow{\left| B \right|}\cos \theta }$

where $\overrightarrow{\left| A \right|},\overrightarrow{\left| B \right|}$ are the magnitudes of the vectors $\overrightarrow{A},\overrightarrow{B}$ respectively and $\theta $ is the angle between $\overrightarrow{A}$ and $\overrightarrow{B}$.

Complete step by step answer:
As explained in the hint, we will solve this problem by using the information given in the question to form two equations using the cosine law for the magnitude of the resultant of two vectors.

The magnitude $\left| \overrightarrow{R} \right|$ of the resultant $\overrightarrow{R}$ of two vectors $\overrightarrow{A}$ and $\overrightarrow{B}$ is given by

$\overrightarrow{\left| R \right|}=\sqrt{{{\overrightarrow{\left| A \right|}}^{2}}+{{\overrightarrow{\left| B \right|}}^{2}}+2\overrightarrow{\left| A \right|}\overrightarrow{\left| B \right|}\cos \theta }$ --(1)

where $\overrightarrow{\left| A \right|},\overrightarrow{\left| B \right|}$ are the magnitudes of the vectors $\overrightarrow{A},\overrightarrow{B}$ respectively and $\theta $ is the angle between $\overrightarrow{A}$ and $\overrightarrow{B}$.

Hence, let us analyze the question.

Let the two vectors with magnitudes $P$ and $Q$ be $\overrightarrow{P}$ and $\overrightarrow{Q}$ respectively and the magnitude of the resultant $\overrightarrow{R}$ be $R$. Let the angle between $\overrightarrow{P}$ and $\overrightarrow{Q}$ be $\phi $.
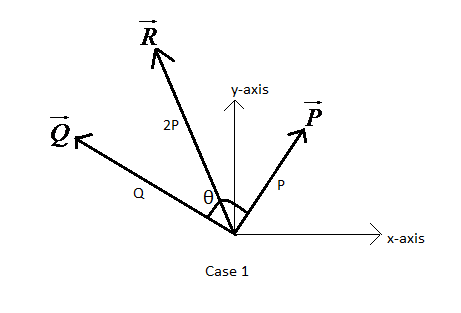
Case 1) $\phi =\theta $, $R=2P$
For this case, using (1), we get,
$2P=\sqrt{{{P}^{2}}+{{Q}^{2}}+2PQ\cos \theta }$

Squaring both sides we get,
${{\left( 2P \right)}^{2}}={{\left( \sqrt{{{P}^{2}}+{{Q}^{2}}+2PQ\cos \theta } \right)}^{2}}$
$\therefore 4{{P}^{2}}={{P}^{2}}+{{Q}^{2}}+2PQ\cos \theta $
$\therefore 4{{P}^{2}}-{{P}^{2}}={{Q}^{2}}+2PQ\cos \theta $
$\therefore 3{{P}^{2}}={{Q}^{2}}+2PQ\cos \theta $ --(2)

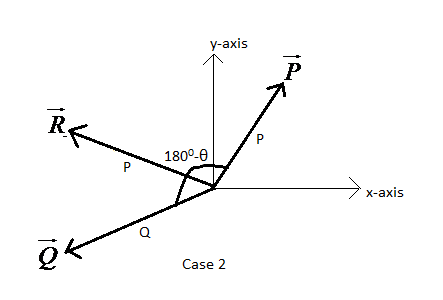
Now, Case 2) $\phi ={{180}^{0}}-\theta ,R=P$
For this case, using (2), we get,
$P=\sqrt{{{P}^{2}}+{{Q}^{2}}+2PQ\cos \left( {{180}^{0}}-\theta \right)}$

Squaring both sides we get,
${{\left( P \right)}^{2}}={{\left( \sqrt{{{P}^{2}}+{{Q}^{2}}+2PQ\cos \left( {{180}^{0}}-\theta \right)} \right)}^{2}}$
$\therefore {{P}^{2}}={{P}^{2}}+{{Q}^{2}}+2PQ\cos \left( {{180}^{0}}-\theta \right)$
$\therefore {{P}^{2}}-{{P}^{2}}={{Q}^{2}}+2PQ\left( -\cos \theta \right)$ $\left( \because \cos \left( {{180}^{0}}-\theta \right)=-\cos \theta \right)$
$\therefore 0={{Q}^{2}}-2PQ\cos \theta $
$\therefore {{Q}^{2}}=2PQ\cos \theta $ ---(3)

Putting (3) in (2), we get
$3{{P}^{2}}={{Q}^{2}}+{{Q}^{2}}=2{{Q}^{2}}$
$\therefore \dfrac{{{P}^{2}}}{{{Q}^{2}}}=\dfrac{2}{3}$
$\therefore {{\left( \dfrac{P}{Q} \right)}^{2}}=\dfrac{2}{3}$

Square rooting both sides, we get,
$\sqrt{{{\left( \dfrac{P}{Q} \right)}^{2}}}=\pm \sqrt{\dfrac{2}{3}}$
$\therefore \dfrac{P}{Q}=\pm \dfrac{2}{3}$
However, $\dfrac{P}{Q}=\dfrac{2}{3}$ . (Since $P$ and $Q$ are magnitudes of vectors and magnitudes are always positive, $P>0,Q>0$. Hence, $\dfrac{P}{Q}>0$)
$\therefore \dfrac{P}{Q}=\dfrac{2}{3}$

Hence, the required ratio is $\dfrac{2}{3}=2:3$.

Note: This problem could also have been solved by drawing diagrams for the two cases with proper orthogonal axes and solving for the components of the vectors along these axes if the angle made by each vector with either one of the axes would have been given in the question. However, this would have been a more indirect method and would result in a lengthier process with a lot of calculations and unnecessary variables. The best method to solving these types of problems would be to use the direct formula for the resultant magnitude, that is, the cosine law for the magnitude of the resultant of two vectors.