Question

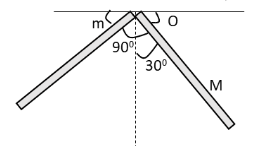
Two Uniform rods of equal length but different masses are rigidly joined to form an L-shaped body, which is then pivoted about O as shown in the figure. If the system is in equilibrium in the shown configuration. Then the ratio \[M/m\] will be:

A. \[2\]
B. \[3\]
C. \[\sqrt 2 \]
D. \[\sqrt 3 \]

Answer 1

Hint:Use the formula for torque acting on an object. This formula gives the relation between the torque, force acting on the object and the perpendicular distance between the point of action of force and centre of the torque. The net torque acting on a system is zero if the system is in equilibrium. Determine the value of torques acting on both the rods and equate the sum of these torques to zero.

Formula used:
The torque \[\tau \] acting on an object is
\[\tau = Fr\] …… (1)
Here, \[F\] is the force acting on the object, \[r\] is a perpendicular distance between the point of action of force and centre of the torque.

Complete step by step answer:
We have given that the mass of the left hand side rod is \[m\], the mass of the right hand side rod is \[M\] and the length of both of the rods is \[L\]. The force acting on both the rods are their weights acting in the downward direction at the centre of their lengths. The torque \[{\tau _m}\] acting on the left hand side rod due to its weight \[mg\] according to equation (1) is,
\[{\tau _m} = mg\dfrac{L}{2}\sin 60^\circ \]

The torque \[{\tau _M}\] acting on the left hand side rod due to its weight \[Mg\] according to equation (1) is
\[{\tau _M} = - Mg\dfrac{L}{2}\sin 30^\circ \]
For the system of two rods to be in equilibrium, the net torque acting on both the rods must be zero.Hence, the sum of the torques acting on the given system is zero.
\[{\tau _m} + {\tau _M} = 0\]

Substitute \[mg\dfrac{L}{2}\sin 60^\circ \] for \[{\tau _m}\] and \[ - Mg\dfrac{L}{2}\sin 30^\circ \] for \[{\tau _M}\] in the above equation.
\[mg\dfrac{L}{2}\sin 60^\circ - Mg\dfrac{L}{2}\sin 30^\circ = 0\]
\[ \Rightarrow m\sin 60^\circ = M\sin 30^\circ \]
\[ \Rightarrow \dfrac{M}{m} = \dfrac{{\sin 60^\circ }}{{\sin 30^\circ }}\]
\[ \Rightarrow \dfrac{M}{m} = \dfrac{{\dfrac{{\sqrt 3 }}{2}}}{{\dfrac{1}{2}}}\]
\[ \therefore \dfrac{M}{m} = \sqrt 3 \]
Therefore, the value of the ratio of masses is \[\sqrt 3 \].

Hence, the correct option is D.

Note: The students may think that the torque acting on the right hand side rod is taken negative and on the left hand side rod is positive. The torque acting on the right hand side is in the clockwise direction. Hence, it is negative. The torque acting on the right hand side is in the anti-clockwise direction. Hence, it is positive.