Question

Two trains leave a railway station at the same time. The first train travels towards west and the second train due north. The first train travels 5 km/hr. faster than the second train. If after two hours they are 50 km apart, find the average speed of each train.

Answer 1

Hint: Here we go through by first assuming the average speed of one train as some variable and by that variable we will find out the average speed of another train. And by the help of Pythagoras theorem in distance we will find out the value of the variables.

Complete step-by-step answer:
Let the average speed of the second train be x km/h.
Thus, the speed of the first train will be (x+5) km/h.
As we know distance traveled is equal to speed multiplied by time. So,
Distance travelled by the first train in two hours =2(x+5) km/h
Distance travelled by the second train in two hours =2x km/h
Now draw the diagram as the trains moved in two direction,

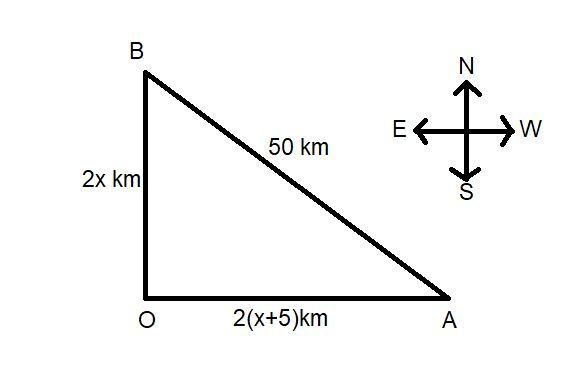
As the first train traveled OA distance and the second train traveled OB distance and after two hours the two trains are 50 km apart i.e. 5o km.
And now by applying Pythagoras theorem we get,
$4{x^2} + 4{(x + 5)^2} = {50^2}$ As we know Pythagoras theorem state that ${(OA)^2} + {(OB)^2} = {(AC)^2}$
$
   \Rightarrow 4{x^2} + 4{x^2} + 40x + 100 = 2500 \\
   \Rightarrow 8{x^2} + 40x - 2400 = 0 \\
   \Rightarrow {x^2} + 5x - 300 = 0 \\
   \Rightarrow (x - 15)(x + 20) = 0 \\
 $
$\therefore $ x=15 an x= -20
Ignore the negative value of the speed. We have,
Speed of the second train was 15 km/hr.
Speed of the first train is (15+5) = 20 km/hr.

Note: - Whenever we face such type of question the key concept for solving the question is to first let assume the speed of train and in the question the two trains are moving in the two perpendicular direction so just make the diagram and it forms a right angle triangle so apply the rule of Pythagoras theorem in their distance by these steps you will get your answers.