
Two towns A and B are 60 km apart. A school is to be built to serve 150 students in town A and 50 students in town B. If the total distance to be travelled by all 200 students is to be as small as possible, then the school be built is \[\]
A. town B \[\]
B.45 km from town A\[\]
C. town A\[\]
D. 45 km from town B\[\]
Answer
575.7k+ views
Hint: We assume the distance of the school to be built from town A as $x$ and then we have the distance of town B from the school to be built as $60-x$. We find the distance that needs to be travelled by all the students of town A as ${{d}_{A}}$, the distance that needs to be travelled by all the students of town as ${{d}_{B}}$ and then total students travelled by all the students from town A and town B $d={{d}_{A}}+{{d}_{B}}$ as an expression in $x$. We find $x$ for the minimum value of $d$ and choose the position of school. \[\]
Complete step-by-step answer:
We are given the question that two towns A and B are 60 km apart. A school is to be built to serve 150 students in town A and 50 students in town B. Let us denote the distance of the school to be built from town A as $x$ and then we have the distance of town B from the school to be built as $60-x$. \[\]
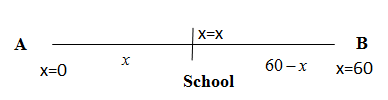
We are also given in the question that there are 150 students in town A and 50 students in town B. So the total distance ${{d}_{A}}$ that will be travelled if the school is built by students of town A is
\[{{d}_{A}}=150\times x=150x\]
The total distance ${{d}_{B}}$ that will be travelled if the school is built by students of town B is
\[{{d}_{B}}=50\times \left( 60-x \right)=3000-50x\]
So the total distance travelled by all the 200 students both from town A and town B is sum of distances travelled by the students of town A and town B which is,
\[\begin{align}
& d={{d}_{A}}+{{d}_{B}}=150x+3000-50x \\
& \Rightarrow d=100x+3000 \\
\end{align}\]
We observe the above equation in order to minimize$d$. We know that distance cannot be negative, so $x\ge 0$. So we shall have minimum $d$ when $x=0$ and at $x=0$ , the position of the school to be built is town A. So the correct option is C. \[\]
So, the correct answer is “Option C”.
Note: We note that we have only considered the distance from town to the school not the returning distance from school to town where we shall have the same answer. We note that critical point the distance function$d\left( x \right)=100x+3000$ is always an increasing function and does not have maxima or minima unless we put some constraints on $x$like in this problem. We can find the maxima or minima of a function using the first and second order derivative test if they exist.
Complete step-by-step answer:
We are given the question that two towns A and B are 60 km apart. A school is to be built to serve 150 students in town A and 50 students in town B. Let us denote the distance of the school to be built from town A as $x$ and then we have the distance of town B from the school to be built as $60-x$. \[\]
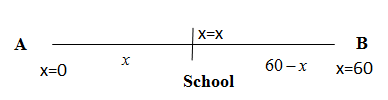
We are also given in the question that there are 150 students in town A and 50 students in town B. So the total distance ${{d}_{A}}$ that will be travelled if the school is built by students of town A is
\[{{d}_{A}}=150\times x=150x\]
The total distance ${{d}_{B}}$ that will be travelled if the school is built by students of town B is
\[{{d}_{B}}=50\times \left( 60-x \right)=3000-50x\]
So the total distance travelled by all the 200 students both from town A and town B is sum of distances travelled by the students of town A and town B which is,
\[\begin{align}
& d={{d}_{A}}+{{d}_{B}}=150x+3000-50x \\
& \Rightarrow d=100x+3000 \\
\end{align}\]
We observe the above equation in order to minimize$d$. We know that distance cannot be negative, so $x\ge 0$. So we shall have minimum $d$ when $x=0$ and at $x=0$ , the position of the school to be built is town A. So the correct option is C. \[\]
So, the correct answer is “Option C”.
Note: We note that we have only considered the distance from town to the school not the returning distance from school to town where we shall have the same answer. We note that critical point the distance function$d\left( x \right)=100x+3000$ is always an increasing function and does not have maxima or minima unless we put some constraints on $x$like in this problem. We can find the maxima or minima of a function using the first and second order derivative test if they exist.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




