Question

Two tangents TP and TQ are drawn to a circle with centre O from an external point T.
Prove that $\angle PTQ = 2\angle OPQ$.

Answer 1

Hint: According to given in the question we have to prove that $\angle PTQ = 2\angle OPQ$ when two tangents TP and TQ are drawn to a circle with centre O from an external point T. So, first of all we have to consider the diagram as given below:

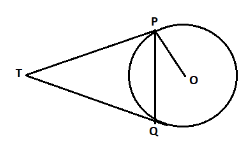
So, first of all we have to make the angels equal to each other as $\angle TQP = \angle TPQ$ Now, as given in the question that line Op is perpendicular to line TP and as we know that tangent at any point of a circle is perpendicular to that radius through point of contact.
Now, we have to obtain the sum of all the angels for the triangle TPQ. Hence, on substituting all the angles we can prove that $\angle PTQ = 2\angle OPQ$

Complete step-by-step answer:
Step 1: First of all as we all know that the length of tangents drawn from the point T to the circle are equal to each other. Hence,

$ \Rightarrow $TP = TQ…………….(1)
Step 2: Now, as mentioned in the solution, hint angles of equal sides are equal to each other. Hence,
$ \Rightarrow \angle TQP = \angle TPQ$………………..(2)
Step 3: Now, as we know that TP is tangent and OP is radius so OP is perpendicular to TP and tangent at any point of a circle is perpendicular to that radius through point of contact. Hence,
$ \Rightarrow \angle OPT = {90^\circ}$
$ \Rightarrow \angle OPQ + \angle TPQ = {90^\circ}$ or,
$ \Rightarrow \angle TPQ = {90^\circ} - \angle OPQ..............(3)$
Step 4: Now, in triangle PTQ as we know that the sum of all angles is ${180^\circ}$. Hence,
$ \Rightarrow \angle TPQ + \angle PQT + \angle QTP = {180^\circ}$
Now, on substituting the angles we obtained in the solution steps. Hence,
$ \Rightarrow {90^\circ} - \angle OPQ + \angle TPQ + \angle QTP = {180^\circ}$
On substituting the values as obtained from expressions (1) and (2),
 $
   \Rightarrow 2({90^\circ} - \angle OPQ) + \angle QTP = {180^\circ} \\
   \Rightarrow {180^\circ} - 2\angle OPQ + \angle PTQ = {180^\circ} \\
   \Rightarrow 2\angle OPQ = \angle PTQ
 $

Hence, with the help of tangents as given in the question we have proved that $\angle PTQ = 2\angle OPQ$

Note: A tangent to a circle is a line that intersects a circle at exactly two points and the tangent must be at a right angled to the radius that intersects that same point.
The tangent touches the circle only at one point and it is perpendicular to the radius since the tangent is a line hence, it also has its equation.