Question

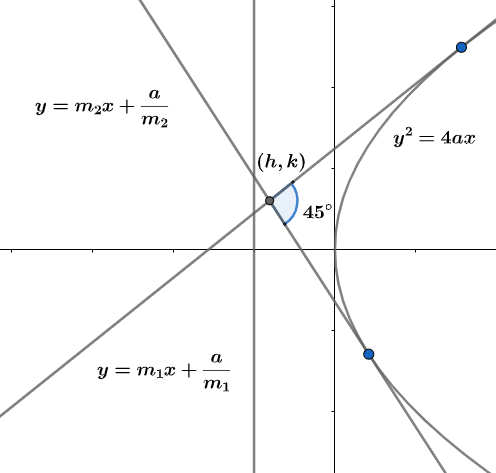
Two tangents to a parabola $ {{y}^{2}}=4ax $ meet at an angle of $ {{45}^{\circ }} $ . Prove that the locus of their point of intersection is the curve $ {{y}^{2}}-4ax={{\left( x+a \right)}^{2}} $ . \[\]

Answer 1

Hint: We take the point of intersection of tangents at one instance as $ \left( h,k \right) $ . We use the general equation of the parabola $ {{y}^{2}}=4ax $ that is $ y=mx+\dfrac{a}{m} $ and put $ \left( h,k \right) $ to get quadratic equation in $ m $ . The roots of the quadratic equation will be the slopes of intersecting tangents $ {{m}_{1}},{{m}_{2}} $ . We use formula for angle $ \theta $ between two lines $ \tan \theta =\dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}} $ and put $ \theta ={{45}^{\circ }} $ and simplify. We replace $ \left( h,k \right) $ by $ \left( x,y \right) $ to get the locus. \[\]

Complete step by step answer:
We are given the equation of parabola opened towards right as
\[{{y}^{2}}=4ax......\left( 1 \right)\]
We know that the equation of any tangent to parabola (1) is given by
\[y=mx+\dfrac{a}{m}.......\left( 2 \right)\]
 Let $ \left( h,k \right) $ be the coordinates of the point of intersection of the tangents meeting at $ {{45}^{\circ }} $ angle as given in the question. Since $ \left( h,k \right) $ lies on the tangent line (2) we have;
\[\begin{align}
  & k=mh+\dfrac{a}{m} \\
 & \Rightarrow h{{m}^{2}}-km+a=0 \\
\end{align}\]
The roots of the above equation say $ {{m}_{1}},{{m}_{2}} $ will be the slopes of intersecting tangents. We use the sum of the roots formula and have;
\[{{m}_{1}}+{{m}_{2}}=\dfrac{-\left( -k \right)}{h}=\dfrac{k}{h}\]
We use product of the roots formula and have;
\[{{m}_{1}}{{m}_{2}}=\dfrac{a}{h}\]
We use the algebraic identity $ {{\left( a+b \right)}^{2}}-{{\left( a-b \right)}^{2}}=4ab $ for $ a={{m}_{1}},b={{m}_{2}} $ to have;
\[\begin{align}
  & {{\left( {{m}_{1}}-{{m}_{2}} \right)}^{2}}={{\left( {{m}_{1}}+{{m}_{2}} \right)}^{2}}-4{{m}_{1}}{{m}_{2}} \\
 & \Rightarrow {{\left( {{m}_{1}}-{{m}_{2}} \right)}^{2}}={{\left( \dfrac{k}{h} \right)}^{2}}-4\left( \dfrac{a}{h} \right) \\
 & \Rightarrow {{\left( {{m}_{1}}-{{m}_{2}} \right)}^{2}}=\dfrac{{{k}^{2}}-4ah}{{{h}^{2}}} \\
 & \Rightarrow {{m}_{1}}-{{m}_{2}}=\pm \dfrac{\sqrt{{{k}^{2}}-4ah}}{h} \\
\end{align}\]
 We know that the angles between two lines $ \theta $ with slopes $ {{m}_{1}},{{m}_{2}} $ is obtained from the equation
\[\tan \theta =\dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}}\]
We put the given $ \theta ={{45}^{\circ }} $ an previously obtained $ {{m}_{1}}{{m}_{2}}=\dfrac{a}{h},{{m}_{1}}-{{m}_{2}}=\pm \dfrac{\sqrt{{{k}^{2}}-4ah}}{h} $ to have;
\[\begin{align}
  & \tan {{45}^{\circ }}=\dfrac{\pm \dfrac{\sqrt{{{k}^{2}}-4ah}}{h}}{1+\dfrac{a}{h}} \\
 & \Rightarrow 1=\pm \dfrac{\sqrt{{{k}^{2}}-4ah}}{h+a} \\
\end{align}\]
We square both side to have;
\[\begin{align}
  & \Rightarrow 1=\dfrac{{{k}^{2}}-4ah}{{{\left( h+a \right)}^{2}}} \\
 & \Rightarrow {{k}^{2}}-4ah={{\left( h+a \right)}^{2}} \\
\end{align}\]
We replace $ \left( h,k \right) $ by $ \left( x,y \right) $ to represent all such points of intersection of tangents $ y={{m}_{1}}x+\dfrac{a}{{{m}_{1}}},y={{m}_{2}}x+\dfrac{a}{{{m}_{2}}} $ as the locus
\[{{y}^{2}}-4ax={{\left( x+a \right)}^{2}}\]
Hence the given statement is proved. \[\]

Note:
We note that the angle $ \theta ={{\tan }^{-1}}\left( \dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}} \right) $ may be acute or obtuse. Since two lines form two pairs of equal opposite angles they will be of measure $ \theta ,{{180}^{\circ }}-\theta $ . We can alternatively solve using parametric points of contact $ \left( at_{1}^{2},2a{{t}_{1}} \right),\left( at_{2}^{2},2a{{t}_{2}} \right) $ of the tangents $ {{t}_{1}}y=x+at_{1}^{2},{{t}_{2}}y=x+at_{2}^{2} $ where the point of intersection is given by $ \left( h,k \right)=\left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right) $ . We can find $ {{t}_{1}}{{t}_{2}},{{t}_{1}}+{{t}_{2}} $ using the formula for angle between lines to have $ \tan \theta =\dfrac{{{t}_{1}}-{{t}_{2}}}{1+{{t}_{1}}{{t}_{2}}} $ and then eliminate $ {{t}_{1}},{{t}_{2}} $ to get the equation in $ h,k $ .