
Two tailors A and B earn ₹150 and ₹200 per day respectively. A can stitch 6 shirts and 4 pants per day, while B can stitch 10 shirts and 4 pants per day. Form an LPP to minimize the labor cost to produce (stitch) at least 60 shirts and 32 pants and solve it graphically.
Answer
558k+ views
Hint: Let x and y be the number of days A and B work respectively to obtain the objective function $ Z = 150x + 200y $
Express the given information in terms of these variables to obtain the LPP.
The lower limits on the number of shirts and pants to be produced give us the remaining constraints.
$ 6x + 10y \geqslant 60 $
$ 4x + 4y \geqslant 32 $
The objective function and the other constraints along with the non-negativity of x and y gives us the required LPP.
Draw the graphs of the lines $ 6x + 10y = 60 $ and $ 4x + 4y = 32 $ to obtain the feasible region.
Find all the vertices of the feasible region by solving these equations.
The solution $ (x,y) $ is one of the vertices of this feasible region.
Complete step by step solution:
Here we have two tailors A and B.
Their earnings are ₹150 and ₹200 per day respectively.
Also, tailor A stitches 6 shirts and 4 pants per day.
Whereas tailor B stitches 10 shirts and 4 pants per day.
We are asked to
1) Form an LPP to minimize the labor cost while producing at least 60 shirts and 32 pants.
2) Solve the LPP graphically
Since the labor cost depends on the number of days, if we optimize the number of days required, we can minimize the labor cost.
So, let $ x $ be the number of days for which tailor A works.
Let $ y $ be the number of days for which tailor B works.
Number of days cannot be negative.
Therefore, we have our first constraint $ x,y \geqslant 0...........(i) $
Our next constraint is on the labor cost involved which we would like to minimize
Total labor cost for a tailor = cost per day $ \times $ number of days
Therefore, for A, we have labor cost $ = 150x $
Similarly, for B, the labor cost $ = 200y $
Thus, the total labor cost $ = 150x + 200y $
This gives us the objective function of our LPP: Minimize $ Z = 150x + 200y...........(ii) $
Minimize $ Z = 150x + 200y $
Subject to constraints
$ 6x + 10y \geqslant 60 $
$ 4x + 4y \geqslant 32 $
$ x,y \geqslant 0 $
This answers the first part of the question.
Consider the equations $ 6x + 10y = 60 $ and $ 4x + 4y = 32 $ to solve the problem graphically.
As we can see these are equations of straight lines, we will need two points of each of these lines to plot their graphs.
Put $ x = 0 $ in $ 6x + 10y = 60 $ , then we get
$
6(0) + 10y = 60 \\
\Rightarrow 10y = 60 \\
\Rightarrow y = 6 \;
$
Now, put $ y = 0 $ in $ 6x + 10y = 60 $ , then we get
$
6x + 10(0) = 60 \\
\Rightarrow 6x = 60 \\
\Rightarrow x = 10 \;
$
Therefore, the points we will use for plotting $ 6x + 10y = 60 $ are $ (0,6) $ and $ (10,0) $
Similarly, by substituting $ x = 0 $ and $ y = 0 $ , we get the points $ (0,8) $ and $ (8,0) $ for $ 4x + 4y = 32 $
Using these points we get the following graph:
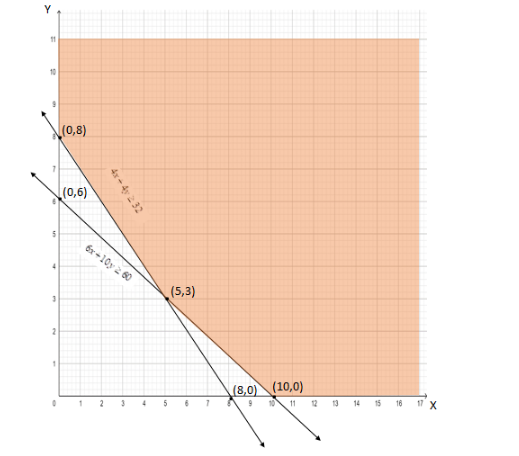
As we have $ \geqslant $ type constraints in the LPP, the feasible region is the unbounded area away from the origin as shown in the above figure (the shaded part).
The optimal solution is obtained using one of the vertices of this feasible region.
So, we need to compute the value of Z at these vertices to find its minimum value.
The vertices of the feasible region are $ D(0,8) $ , $ C(10,0) $ and $ E(x,y) $ .
To find the coordinates of E, we solve the equations $ 6x + 10y = 60 $ and $ 4x + 4y = 32 $ simultaneously
On simplifying further, these equations become $ 3x + 5y = 30 $ and $ x + y = 8 $
Put $ y = 8 - x $ in $ 3x + 5y = 30 $
Then we have
$
3x + 5(8 - x) = 30 \\
\Rightarrow 3x + 40 - 5x = 30 \\
\Rightarrow 2x = 10 \\
\Rightarrow x = 5 \;
$
Therefore,\[y = 8 - x = 8 - 5 = 3\]
$ \Rightarrow E \equiv (3,5) $
Let’s calculate the value of Z.
Therefore, Z is minimum at the point $ E(5,3) $ , i.e. when $ x = 5 $ and $ y = 3 $ , and the minimum value of Z is ₹1350
So, the correct answer is “ ₹1350”.
Note: Students tend to assume that for every minimization question, the feasible region is unbounded. However, this is not true. The boundary of the feasible region depends on the set of constraints which is used to draw the graph.
Express the given information in terms of these variables to obtain the LPP.
The lower limits on the number of shirts and pants to be produced give us the remaining constraints.
$ 6x + 10y \geqslant 60 $
$ 4x + 4y \geqslant 32 $
The objective function and the other constraints along with the non-negativity of x and y gives us the required LPP.
Draw the graphs of the lines $ 6x + 10y = 60 $ and $ 4x + 4y = 32 $ to obtain the feasible region.
Find all the vertices of the feasible region by solving these equations.
The solution $ (x,y) $ is one of the vertices of this feasible region.
Complete step by step solution:
Here we have two tailors A and B.
Their earnings are ₹150 and ₹200 per day respectively.
Also, tailor A stitches 6 shirts and 4 pants per day.
Whereas tailor B stitches 10 shirts and 4 pants per day.
We are asked to
1) Form an LPP to minimize the labor cost while producing at least 60 shirts and 32 pants.
2) Solve the LPP graphically
Since the labor cost depends on the number of days, if we optimize the number of days required, we can minimize the labor cost.
So, let $ x $ be the number of days for which tailor A works.
Let $ y $ be the number of days for which tailor B works.
Number of days cannot be negative.
Therefore, we have our first constraint $ x,y \geqslant 0...........(i) $
Our next constraint is on the labor cost involved which we would like to minimize
Total labor cost for a tailor = cost per day $ \times $ number of days
Therefore, for A, we have labor cost $ = 150x $
Similarly, for B, the labor cost $ = 200y $
Thus, the total labor cost $ = 150x + 200y $
This gives us the objective function of our LPP: Minimize $ Z = 150x + 200y...........(ii) $
Minimize $ Z = 150x + 200y $
Subject to constraints
$ 6x + 10y \geqslant 60 $
$ 4x + 4y \geqslant 32 $
$ x,y \geqslant 0 $
This answers the first part of the question.
Consider the equations $ 6x + 10y = 60 $ and $ 4x + 4y = 32 $ to solve the problem graphically.
As we can see these are equations of straight lines, we will need two points of each of these lines to plot their graphs.
Put $ x = 0 $ in $ 6x + 10y = 60 $ , then we get
$
6(0) + 10y = 60 \\
\Rightarrow 10y = 60 \\
\Rightarrow y = 6 \;
$
Now, put $ y = 0 $ in $ 6x + 10y = 60 $ , then we get
$
6x + 10(0) = 60 \\
\Rightarrow 6x = 60 \\
\Rightarrow x = 10 \;
$
Therefore, the points we will use for plotting $ 6x + 10y = 60 $ are $ (0,6) $ and $ (10,0) $
Similarly, by substituting $ x = 0 $ and $ y = 0 $ , we get the points $ (0,8) $ and $ (8,0) $ for $ 4x + 4y = 32 $
Using these points we get the following graph:

As we have $ \geqslant $ type constraints in the LPP, the feasible region is the unbounded area away from the origin as shown in the above figure (the shaded part).
The optimal solution is obtained using one of the vertices of this feasible region.
So, we need to compute the value of Z at these vertices to find its minimum value.
The vertices of the feasible region are $ D(0,8) $ , $ C(10,0) $ and $ E(x,y) $ .
To find the coordinates of E, we solve the equations $ 6x + 10y = 60 $ and $ 4x + 4y = 32 $ simultaneously
On simplifying further, these equations become $ 3x + 5y = 30 $ and $ x + y = 8 $
Put $ y = 8 - x $ in $ 3x + 5y = 30 $
Then we have
$
3x + 5(8 - x) = 30 \\
\Rightarrow 3x + 40 - 5x = 30 \\
\Rightarrow 2x = 10 \\
\Rightarrow x = 5 \;
$
Therefore,\[y = 8 - x = 8 - 5 = 3\]
$ \Rightarrow E \equiv (3,5) $
Let’s calculate the value of Z.
| Point | Z |
| $ D(0,8) $ | $ Z = 150(0) + 200(8) = 1600 $ |
| $ C(10,0) $ | $ Z = 150(10) + 200(0) = 1500 $ |
| $ E(5,3) $ | $ Z = 150(5) + 200(3) = 750 + 600 = 1350 $ |
Therefore, Z is minimum at the point $ E(5,3) $ , i.e. when $ x = 5 $ and $ y = 3 $ , and the minimum value of Z is ₹1350
So, the correct answer is “ ₹1350”.
Note: Students tend to assume that for every minimization question, the feasible region is unbounded. However, this is not true. The boundary of the feasible region depends on the set of constraints which is used to draw the graph.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




