Question

Two supplementary angles differ by \[48^\circ \]. Find the angles.

Answer 1

Hint:
We will by considering the measures of the unknown angles as \[x^\circ \]and \[y^\circ \]. The given angles are supplementary, so will use the supplementary angles property and the condition given to find the unknown angles.

Complete step by step solution:
Let \[AOB\] be a straight line and \[OC\] be a ray standing on the line\[AOB\].
Let us consider the measures of the unknown angles as \[x^\circ \]and \[y^\circ \]i.e., let \[\angle AOC = x^\circ \] and \[\angle BOC = y^\circ \]

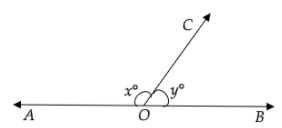
It is given that the two angles whose measures we have assumed to be \[x^\circ \]and \[y^\circ \] are supplementary. Two angles are said to be supplementary if the sum of their measures is \[180^\circ \].
Hence, applying this to the angles \[\angle AOC\] and \[\angle BOC\], we get
\[\angle AOC + \angle BOC = 180^\circ \]\[\angle AOC + \angle BOC = 180^\circ \] ……….\[(1)\]
We have assumed \[\angle AOC = x^\circ \] and \[\angle BOC = y^\circ \]. Let us substitute this in equation \[(1)\]. We get,
\[x^\circ + y^\circ = 180^\circ \]……….\[(2)\]
It is also given that the two angles differ by \[48^\circ \]. This means that one angle is greater than the other by \[48^\circ \]. Let us take \[\angle AOC > \angle BOC\]. Now, the difference in their measure is \[48^\circ \] i.e.,
\[\angle AOC - \angle BOC = 48^\circ \] ……..\[(3)\]
Using \[\angle AOC = x^\circ \] and \[\angle BOC = y^\circ \] in equation \[(3)\], we get
\[x^\circ - y^\circ = 48^\circ \] ……….\[(4)\]
From equation \[(4)\], we also get
\[x^\circ = y^\circ + 48^\circ \] ……….\[(5)\]
Substituting equation \[(5)\] in equation \[(2)\], we have
\[(y^\circ + 48^\circ ) + y^\circ = 180^\circ \]
Adding like terms on the LHS, we get
\[2y^\circ + 48^\circ = 180^\circ \]
Taking \[48^\circ \] from the LHS to the RHS, we have
\[2y^\circ = 180^\circ - 48^\circ = 132^\circ \]
Dividing both sides by 2, we get
\[\begin{array}{l}\dfrac{{2y^\circ }}{2} = \dfrac{{132^\circ }}{2}\\ \Rightarrow y^\circ = 66^\circ \end{array}\]
Substituting \[y^\circ = 66^\circ \] in equation \[(5)\], we get
\[x^\circ = 66^\circ + 48^\circ = 114^\circ \]

Therefore, the angles are \[\angle AOC = 114^\circ \] and \[\angle BOC = 66^\circ \].

Note:
When two angles are said to be supplementary, two cases arise:
1) One angle is an obtuse angle (i.e., greater than \[90^\circ \]) and the other is an acute angle (i.e., less than \[90^\circ \])
2) Both angles are right angles (i.e., \[90^\circ \])