Question

Two streams of water flow through the U-shaped tubes shown. The tube on the left has a cross-sectional area $A$ and the speed of the water flowing through it is $v$, the tube on the right has a cross-sectional area $A' = \dfrac{A}{2}$. If the net force on the tube assembly is zero. What must be the value $v'$ of the water flowing through the tube on the right? Neglect gravity and assume that the speed of the water in each tube is the same upon entry and exit.

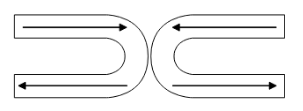
A. $\dfrac{1}{2}v$
B. $v$
C. $\sqrt 2 v$
D. $2v$

Answer 1

Hint: We have two U-shaped tubes and the one on the right has a cross-sectional area half of that of the one on the left and we need to find the relation between the velocities of both the tubes. We need to calculate the change in momentum of both the tubes for finding the required relation.

Complete step by step answer:
Firstly for the tube on the left we have the rate of change of momentum given by
$\Delta p = m(v - ( - v))$
The initial velocity of the tube is in the positive direction and the final velocity will be in the negative direction. By solving the above equation we get
$\Delta p = 2mv = 2\rho {\rm A}{v^2}$
Since the rate of change of volume of a liquid is given by the product of the velocity of the liquid and its cross-sectional area. Similarly, for the tube at the right, we have the rate of change of momentum given by
$\Delta p' = m'( - v' - (v')) = - 2\rho A'v{'^2}$

We know that the rate change of momentum is equal to the force applied and it is given that the net force applied on the system is zero and therefore the force or the rate of change of momentum of the tube should be equal. Hence we have
$\Delta p = \Delta p'$
Substituting the values we get
$2\rho A{v^2} = 2\rho A'v{'^2}$
Substituting the value of the cross-sectional area of the right tube in terms of the cross-sectional of the left tube we get
$\rho A{v^2} = \rho \dfrac{A}{2}v{'^2}$
$\Rightarrow 2{v^2} = v{'^2}$
$\therefore v' = \sqrt 2 v$ which is the required relation.

Hence option C is the correct answer.

Note: The initial and the final velocity of a liquid in a U-shaped tube is given by the direction of the liquid entering the tube and direction of the liquid leaving the tube respectively and hence it is taken opposite. And since we have water flowing through the assembly given, we have taken the same densities for both the tubes while comparing since it has the same liquid.