Question

Two straight roads intersect at an angle of $ {{60}^{\circ }} $ . A bus on one road is 2 km away from the intersection and a car on the other is 3 km away from the intersection; then the direct distance between the two vehicles is \[\]
A.1 km\[\]
B. $ \sqrt{2} $ km \[\]
C.4 km \[\]
D. $ \sqrt{7} $ km\[\]

Answer 1

Hint: We denote the point of intersection of roads as A, the position of the bus as B and the position of the car as C. We use the law of cosine for any triangle $ {{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc\cos A $ and find the required unknown $ a=BC $ using the given data in the question $ b=AC=3,c=AB=2,A={{60}^{\circ }} $ .\[\]

Complete step-by-step answer:

We know from the trigonometric ratios in a right angled triangle that the cosine of an angle is the ratio of side adjacent to the angle say $ \theta $ (excluding hypotenuse) to the hypotenuse $ h $ . So we have cosine of angle $ \theta $
\[\cos \theta =\dfrac{b}{h}\]
We know from the law of cosines that lengths of sides of a triangle are related with cosines of its angles. If we have in triangle ABC the length of the sides opposite to the angles $ A,B,C $ as $ a,b,c $ then the law of cosines are given by
\[\begin{align}
  & {{c}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\cos C \\
 & {{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc\cos A \\
 & {{b}^{2}}={{c}^{2}}+{{a}^{2}}-2ac\cos B \\
\end{align}\]

We are given in the two straight roads intersect at angle of $ {{60}^{\circ }} $ . Let the point of intersection be A. We are also given that A bus on one road is 2 km away from the intersection and a car on the other is 3 km away from the inter-section. Let us denote the position of the bus as B and the position of the car as C. \[\]

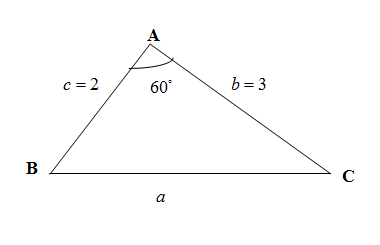
So we have $ c=AB=2 $ km and $ b=AC=3 $ km. We are asked to find in the question the direct distance between the two vehicles which $ BC=a $ . We use the law of cosine for the unknown length of side $ a $ and have,
\[\begin{align}
  & {{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc\cos A \\
 & \Rightarrow {{a}^{2}}={{2}^{2}}+{{3}^{2}}-2\times 2\times 3\times \cos {{60}^{\circ }} \\
 & \Rightarrow {{a}^{2}}=13-12\times \dfrac{1}{2}=7 \\
 & \Rightarrow a=\sqrt{7} \\
\end{align}\]
So the distance between ships is $ \sqrt{7} $ m and the correct option is D. \[\]


So, the correct answer is “Option D”.

Note: We have rejected negative signs on square root $ \sqrt{7} $ because length is always a positive quantity. We must be careful of law of cosine from law of sine which states that lengths of the sides are in proportion with the sine of angle opposite to them which means $ \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C} $ .